Радиус описанной около правильного шестиугольника окружности больше радиуса окружности,вписанной в этот шестиугольник,на 1.
Найдите сторону данного шестиугольника.
264
272
Ответы на вопрос:
1)
R- радиус окружности, описанной около правильного n-угольника со стороной а
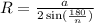
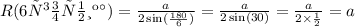
2)
r- радиус окружности вписанной в правильный n-угольник со стороной а
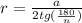
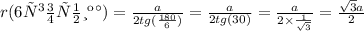
3)
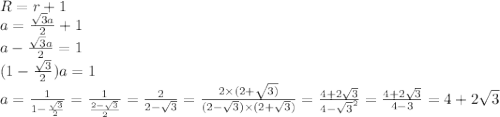
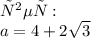
или приблизительно 7,4641
R- радиус окружности, описанной около правильного n-угольника со стороной а
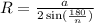
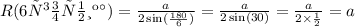
2)
r- радиус окружности вписанной в правильный n-угольник со стороной а
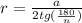
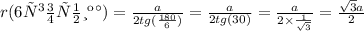
3)
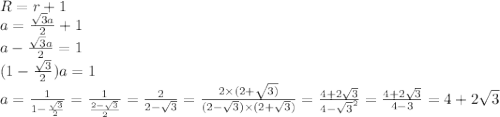
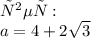
или приблизительно 7,4641
угол abm = углу cbm (т.к. bm - биссектриса угла abc) угол abm = углу bma (накрестлежащие углы при параллельных bc и ad секущей bm) значит угол abm = углу bma, треугольник abm - равнобедренный, след-но am=ab=24 рассмотрим треуг-к abc. т.к биссектриса внутреннего угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам, то an: nc = ab: bc, an: nc=24/40=3/5
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Геометрия
-
На окружности заданной уравнением X2+Y2 =169 найдите точки с абсциссой...
 linov31018.06.2023 01:04
linov31018.06.2023 01:04 -
2. [3] Стороны прямоугольника равны 5 см и 10 см. а) Найдите ширину прямоугольника,...
 йщз25.09.2020 05:10
йщз25.09.2020 05:10 -
Запишіть рівняння прямої, яка симетрична прямій у = х - 2 відносно осі...
 Шоце21.03.2023 13:57
Шоце21.03.2023 13:57 -
Геометрия мыклячедчожючочюряпбябр...
 sveta19772011owor7w13.01.2022 16:46
sveta19772011owor7w13.01.2022 16:46 -
Прямая пересекает стороны треугольника АВС в точках М и К соответственно...
 LyVlAr02.12.2020 00:59
LyVlAr02.12.2020 00:59 -
Доказать, Найти параллельные прямые, И докозать что они параллельные....
 danilkudo42311.06.2020 11:07
danilkudo42311.06.2020 11:07 -
В рав¬но¬бед¬рен¬ном тре¬уголь¬ни¬ке ABC с ос¬но¬ва¬ни-ем AC внеш¬ний...
 orororoyowf77q04.10.2020 00:28
orororoyowf77q04.10.2020 00:28 -
Площини в і ф перпендикулярні та перетинаються по прямій т. Площина а...
 Макс111111м21.05.2021 18:48
Макс111111м21.05.2021 18:48 -
В равнобедренном треугольнике ASF с основанием Af на сторонах AS, SF,...
 daniilnz129.06.2023 10:29
daniilnz129.06.2023 10:29 -
Точка пересечения O — серединная точка для обоих отрезков KE и LM. Найди...
 коля82702.12.2020 10:37
коля82702.12.2020 10:37

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
