( )ОЧЕНЬ АВС-равнобедренный треугольник с основанием АС. Вне треугольника соответственно на лучах АВ и СВ лежат точки К и Е так,что ВК=ВЕ,точка О- середина основания. Докажите что треугольник ЕКО является равнобедренным.

162

479

Посмотреть ответы 3

Ответы на вопрос:

soficaflymi

Геометрия

4,4(4 оценок)

Так как КВ = ВЕ и АВ = ВС => АК= ЕС.

Так как КВ = ВЕ и АК = ЕС => КО = ОЕ, так О - середина АС.

=> треугольник ЕОК - равнобедренный. (КО = ОЕ)

Ч.Т.Д.

Sasha808621

Геометрия

4,4(91 оценок)

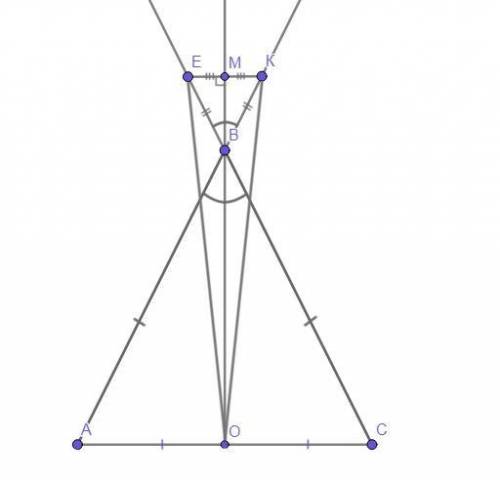
Чертёж смотрите во вложении.

Дано:

ΔАВС - равнобедренный (АС - основание).

Точка К ∈ лучу АВ.

Точка Е ∈ лучу СВ.

ВК = ЕВ.

О - середина АС.

Доказать:

ΔЕКО - равнобедренный.

Доказательство:

Рассмотрим ΔАВС - равнобедренный. Соединим вершину В и точку О. ВО - медиана, проведённая к основанию, а значит, также, биссектриса ∠АВС (по свойству равнобедренного треугольника).

∠АВС = ∠ЕВК как вертикальные, и если мы продлим биссектрису ВО до пересечения стороны ЕК в точке М, то она также будет биссектрисой ∠ЕВК (так как биссектрисы вертикальных углов лежат на одной прямой).

Рассмотрим ΔЕВК - равнобедренный (ВК = ЕВ по условию). ЕК - его основание, и к ней проведена биссектриса ВМ, а значит ВМ⊥ЕК и ЕМ = МК (ВМ - медиана и высота по свойству равнобедренного треугольника).

Рассмотрим весь ΔЕКО. Так как ОМ - медиана и высота одновременно, то ΔЕКО - равнобедренный (по признаку равнобедренного треугольника).

ответ: что требовалось доказать.

( )ОЧЕНЬ АВС-равнобедренный треугольник с основанием АС. Вне треугольника соответственно на лучах АВ

diko2009

Геометрия

4,7(94 оценок)

ответ 110 (должно быть правельно)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.