Регистрация Спросить otvet5GPT
Ритка069
25.01.2023 23:31
Математика
Есть ответ 👍

11 студентов написали тест.Учитель проверил работы и заметил, что для любых двух во теста, найдутся хотя бы 6 студентов, каждый из которых ответил правильно ровно на один из этих двух во Докажите, что в тексте было не более 12 во

127
348
Посмотреть ответы 2

Ответы на вопрос:

kristpan2004p0c22v
kristpan2004p0c22v
4,5(1 оценок)

Представим себе двудольный граф: слева вершины, обозначающие студентов, справа — во Если студент ответил на во то между этим студентом и этим во проведем ребро.

Рассмотрим первую пару во Для них по условию найдется хотя бы 6 студентов, каждый из которых ответил правильно ровно на один из этих двух во Пусть это множество из хотя бы 6 студентов называется 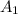A_{1}. Тогда остальных студентов (тех, что не удовлетворяют описанному требованию) не больше 5 — это множество 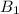B_{1}. Рассмотрим следующую пару во попарно отличных от предыдущих). Тогда 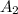A_{2} имеет с 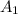A_{1} хотя бы одно пересечение. Поэтому для пары 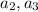a_{2},a_{3} будет хотя бы одно ребро из множества 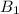B_{1}. Рассматривая далее пары 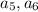a_{5},a_{6} и соответственно пары 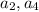a_{2},a_{4} "берем" еще один элемент из 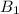B_{1}. Так можно продолжать до тех пор, пока все элементы из 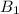B_{1}, коих не больше пяти, не будут взяты. То есть всего можно добавить 2*5=10 во дополнительно к 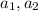a_{1}, a_{2}. То есть всего не более 12.

Примечание: множество 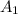A_{1} делится на два множества, из каждого идут ребра к во но из каждого к ровно одному. Для того, чтобы мы могли всегда изымать элементы из 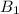B_{1} надо всего лишь без ограничения общности потребовать, чтобы ребро из 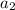a_{2} шло в наибольшее из множеств, на которое делится 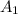A_{1}. Тогда наименьшее из этих множеств деления не превосходит 5.

Tina19977
Tina19977
4,5(88 оценок)
1)выполните действия : а)23 11\20 +15 11\15=38+(11/20+11/15)=38 + (33/60+44/60)=39 17/60 б)60-31 16\35 - 14 17\21 60-31 16/35=28 19/35 28 19/35-14 17/21=14+(19/35-17/21)= 14+(57/105-85/105)=14-28/105=13 77/105 в)27 17\55 - 19,6 + 16 13\22 27 17/55-19,6=27 17/55-19 3/5= 8+(17/55-33/55)=8 -16/55=7 39/55 2)решите уравнения 20 - ( 13 17\35 - х)= 13 27\28 -(13 17/35-x)=13 27/28-20 -13 17/35+x= -6 1/28 x= 13 17/35-6 1/28 x=7 + (68/140-5/140)=7 63/140

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS