NiKaEmpty

28.08.2020 20:12

Математика

Есть ответ 👍

На окружности отмечено 2020 точек. Лягушонок прыгает с одной отмеченной точки на другую, двигаясь по часовой стрелке. За один прыжок он может перепрыгнуть через 99 или через 100 отмеченных точек. Сможет ли лягушонок побывать во всех отмеченных точках ровно по одному разу и вернуться в ту же точку, с которой стартовал?

199

357

Посмотреть ответы 2

Ответы на вопрос:

натали524

Математика

4,6(33 оценок)

Пусть лягушонок стартует в точке 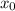$x_{0}$ . Тогда, если какие-то две точки повторились, то лягушонок побывал также в точке 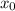$x_{0}$ дважды, т.е. мы попали в цикл. Если мы покажем, что уравнение 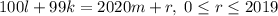$100l+99k=2020m+r,\; 0\leq r\leq 2019$ имеет решение при любом , то цикл будет состоять из всех точек, и лягушонок побывает во всех точках по одному разу, а затем вернется в точку $x_{0}$ ;

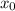Докажем для начала, что если существует решение для остатков 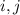i,j , то существует решение для остатка 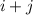i+j . Это вполне очевидно сложим два уравнения для остатков 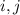i,j . Теперь, в частности, если существует решение для 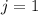j=1 , то существует решение для всех остатков. То есть нам надо решить диофантово уравнение 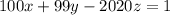100x+99y-2020z=1 ; Для этого сразу положим 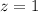z=1 ; Пусть y=21 ;

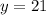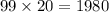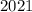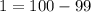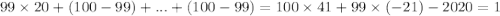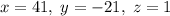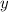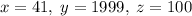Тогда из числа $99\times 20=1980$ нам нужно получить число 2021 ; Но мы умеем прибавлять единицу: 1=100-99 . То есть $99\times 20 +(100-99)+...+(100-99)=100\times41+99\times (-21)-2020=1$ ; Иными словами, получили решение $x=41,\;y=-21,\;z=1$ , но нам нужно решение в натуральных числах. Не во добавим к 2020, а к добавим 99. Получим решение: $x=41,\; y=1999,\; z=100$ .

Итак, план действий следующий.

Пусть мы находимся в точке 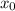$x_{0}$ . Прыгаем 41 раз на 100 и 1999 раз на 99. Теперь мы в точке 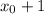$x_{0}+1$ . Таким образом, мы посетим все точки.

ладдщв

Математика

4,7(87 оценок)

80-30=50

30-16=27

27-2=25(осталось нетехранилище)

Если не правильно тогда просите

Пошаговое объяснение:

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.