9Тимур1111111121

21.07.2021 15:10

Есть ответ 👍

с Дифф.ур. Найдите решение уравнения y'=(2-y)tgt, удовлетворяющее начальному условию y(0)=10. В ответе укажите его значение при $t=\pi/3 $

297

374

Посмотреть ответы 2

Ответы на вопрос:

privet45

Математика

4,4(36 оценок)

ответ: y(t) = 10cos(t), y(π/3) = 5

Пошаговое объяснение:

Найдите решение уравнения y'=(2-y)tgt, удовлетворяющее начальному условию y(0)=10. В ответе укажите его значение при t=pi/3

Данное дифференциальное уравнение первого порядка с разделяющимися переменными

y' = (2 - y)tgt

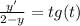
$\frac{y'}{2-y}=tg(t)$

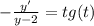
$-\frac{y'}{y-2}=tg(t)$

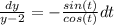
$\frac{dy}{y-2}=-\frac{sin(t)}{cos(t)} dt$

Интегрируем обе части уравнения

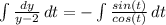
$\int\limits{\frac{dy}{y-2}}} \, dt =-\int\limits{\frac{sin(t)}{cos(t)}} \, dt$

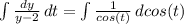
$\int\limits{\frac{dy}{y-2}}} \, dt =\int\limits{\frac{1}{cos(t)}} \, dcos(t)$

lny = lncos(t) + lnC

y(t) = C·cos(t)

Находим константу С при начальном условии y(0)=10

y(0) = C·cos(0) = C = 10

Поэтому искомую функцию можно записать как

y(t) = 10cos(t)

Найдем ее значение при t = π/3

y(π/3) = 10cos(π/3) = 10·(1/2) = 5

dsassaraf

Математика

4,4(45 оценок)

$37x = 259 \\ x = \frac{259}{37} \\ x = 7$

$(38 + b) \div 12 = 840 \\ 38 + b = 840 \times 12 \\ 38 + b = 10080 \\ b = 10080 - 38 \\ b = 10042$

$252 \div y = 21 \\ y = 252 \div 21 \\ y = 12$

$140p - 30 = 630 \\ 140p = 30 + 630 \\ 140p = 660 \\ p = 660 \div 140 \\ p = 4 \frac{5}{7}$

$(43 - s) \div 17 = 289 \\ 43 - s = 17 \times 289 \\ 43 - s = 4913 \\ s = 43 - 4913 \\ s = - 4870$

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.