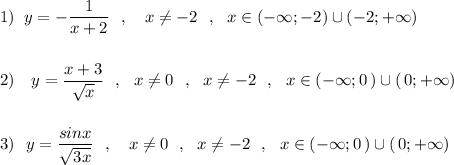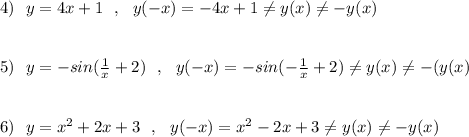Регистрация Спросить otvet5GPT
AlexisA031117
11.08.2020 06:12
Алгебра
Есть ответ 👍

1.Найти область определения следующих функций:а)
а) y=-1/x+2
б) y=x+3/корень из x
в) y=sin x/корень из 3x
2.Исследовать функцию на четность (нечетность):
а) y=-4x+1
б) y=-sin(1/x+2)
в) y=x^2+2x+3

212
331
Посмотреть ответы 2

Ответы на вопрос:

asvazy123
asvazy123
4,4(8 оценок)

1)\; \; y=-\dfrac{1}{x+2}\ \ ,\ \ \ x\ne -2\ \ ,\ \ x\in (-\infty ;-2)\cup(-2;+\infty)\\\\\\2)\ \ \ y=\dfrac{x+3}{\sqrt{x}}\ \ ,\ \ x\ne 0\ \ ,\ \ x\ne -2\ \ ,\ \ x\in (-\infty ;0\, )\cup(\, 0;+\infty)\\\\\\3)\ \ y=\dfrac{sinx}{\sqrt{3x}}\ \ ,\ \ \ x\ne 0\; \ ,\ \ x\ne -2\ \ ,\ \ x\in (-\infty ;0\, )\cup(\, 0;+\infty )

4)\ \ y=4x+1\ \ ,\ \ y(-x)=-4x+1\ne y(x)\ne -y(x)\\\\\\5)\ \ y=-sin(\frac{1}{x}+2)\ \ ,\ \ y(-x)=-sin(-\frac{1}{x}+2)\ne y(x)\ne -(y(x)\\\\\\6)\ \ y=x^2+2x+3\ \ ,\ \ y(-x)=x^2-2x+3\ne y(x)\ne -y(x)

Ни одна функция не является ни чётной, ни нечётной .

LonelyOne
LonelyOne
4,5(83 оценок)
Решение. запишем уравнениe касательной в общем виде: yk   = y0   + y'(x0)(x - x0) по условию x0   = 1, тогда y0   = -1 теперь найдем производную: y' = (2(x^2)-3)' = 4x следовательно: f'(1) = 4 *  1 = 4 в результате имеем: yk   = y0   + y'(x0)(x - x0) yk   = -1 + 4(x - 1) или yk   = -5+4x

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS