Регистрация Спросить otvet5GPT
Gelia1111
16.02.2021 09:12
Математика
Есть ответ 👍

На плоскости лежат два шара радиусами 1 и 2. шары касаются. вычислите: а) расстояние между точками касания шаров плоскости; б) расстояние от точки касания шаров до плоскости

144
392
Посмотреть ответы 3

Ответы на вопрос:

ксения23242526
ксения23242526
4,7(17 оценок)

Тут можно ввести прямоугольную систему координат, где оси - это прямые, по которым пересекаются плоскости. Тогда координаты центра первого шара (1,1,1). А в зависимости от количества "минусов" в координатах центра второго шара (т.е. от октанта, в котором он расположен) возможны 4 случая:

1) Координаты центра (2,2,2). Расстояние равно √((2-1)²+(2-1)^2+(2-1)²)=√3

2) Координаты центра (-2,2,2). Расстояние равно √((2+1)²+(2-1)^2+(2-1)²)=√11

3) Координаты центра (-2,-2,2). Расстояние равно √((2+1)²+(2+1)^2+(2-1)²)=√19

4) Координаты центра (-2,-2,-2). Расстояние равно √((2+1)²+(2+1)^2+(2+1)²)=3√3

AmeliandeAmeliande
AmeliandeAmeliande
4,4(13 оценок)

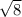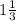
а)\sqrt{8} б)1\frac{1}{3}

Пошаговое объяснение:

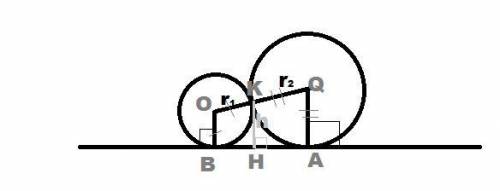
а) Расстояние между точками касания шаров равно AB

OW⊥OB

OB⊥AB

AB⊥AW

AW⊥OW ⇒ OBAW - прямоугольник

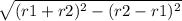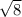
⇒ AB=OW ⇒ AB= √(OQ²-QW²) по т. пифагора =\sqrt{(r1+r2)^2-(r2-r1)^2} = \sqrt{8}

б)KN||QW ⇒∠OKN = ∠OQW (соотв. углы)

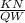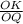
∠KON - общий ⇒треугольники ΔOKN и ΔOQW подобны ⇒ \frac{KN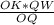}{QW} =\frac{OK}{OQ}

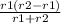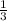
KN= \frac{OK*QW}{OQ} = \frac{r1(r2-r1)}{r1+r2}=\frac{1}{3}

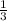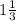
KH= KN+NH = \frac{1}{3}+r₁=1\frac{1}{3}


На плоскости лежат два шара радиусами 1 и 2. шары касаются. вычислите: а) расстояние между точками к
Сашенькадельфинчик
Сашенькадельфинчик
4,7(53 оценок)

ответ:

пошаговое объяснение:

s = 105,6км

v (теч.р.) = 4км/ч

t = 1,6ч

v (моторной лодки) = одинаковый.

1)

s = (1,6(х+4)) + (1,6(х-4)) = 105,6

1,6х+59,2 + 1,6х-59,2 = 105,6

3,2х = 105,6

х = 33км/ч -- v (моторной лодки)

2)

s = (1,6*(33+4)) = 1,6*37 = 59,2 -- s проплывшая по течению

3)

s = (1,6*(33-4)) = 1,6*29 = 46,4 -- s проплывшая против течения

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS