Регистрация Спросить otvet5GPT
mikki255
01.02.2023 03:29
Геометрия
Есть ответ 👍

Даны координаты вершин четырехугольника ABCD:
А (2;4); В(4;6); C(-2;5); D(-3;1)
Написать уравнения прямых АС и BD​

283
324
Посмотреть ответы 2

Ответы на вопрос:

mottorinanadia7
mottorinanadia7
4,4(20 оценок)

х+4у-18=0 - уравнение прямой АС в общем виде.

5х-7у+22=0 - уравнение прямой BD  в общем виде.

Объяснение:

Уравнение прямой АС найдем по формуле:

Умножим обе части на (-4):

х-2=(-4)(у-4)

х-2=-4у+16

х=-4у+16+2

х=-4у+18

Или х+4у-18=0 - уравнение прямой АС в общем виде.

Уравнение прямой BD найдем по формуле:

Умножим на (-1) обе части. Получим

. Умножим на 35 обе части. Получим

5(х-4)=7(у-6)

5х-20=7у-42

5х-7у-20+42=0

5х-7у+22=0 - уравнение прямой BD  в общем виде.


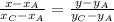
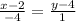
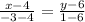
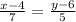
Даны координаты вершин четырехугольника ABCD:А (2;4); В(4;6); C(-2;5); D(-3;1)Написать уравнения пря
Даны координаты вершин четырехугольника ABCD:А (2;4); В(4;6); C(-2;5); D(-3;1)Написать уравнения пря
Даны координаты вершин четырехугольника ABCD:А (2;4); В(4;6); C(-2;5); D(-3;1)Написать уравнения пря
Даны координаты вершин четырехугольника ABCD:А (2;4); В(4;6); C(-2;5); D(-3;1)Написать уравнения пря
Рафаэлла2004
Рафаэлла2004
4,7(24 оценок)
Пусть   ак - биссектриса треугольника авс  , вм - его  медиана.  т.к. биссектриса треугольника авм перпендикулярна стороне вм, она является его высотой. если биссектриса треугольника совпадает с высотой, она является и его  медианой,⇒ треугольник вам - равнобедренный.  ав=ам. вм - медиана треугольника  авс, ⇒   ав=ам=мс, и ас=2 ав.  пусть средняя по длине сторона равна х  если предположить, что ав - средняя сторона, то ас=х+1, вс=х-1 тогда ас=2х=х+1, откуда х=1, и вс=1-1=0, чего быть не может.  ⇒вс- средняя сторона.  вс=х, ас=х+1, ав=х-1  ас=2(х-1)=2х-2  2х-2=х+1  ⇒х=3  вс=3  ав=3-1=2  ас=3+1= 4 - это наибольшее значение самой длинной стороны

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS