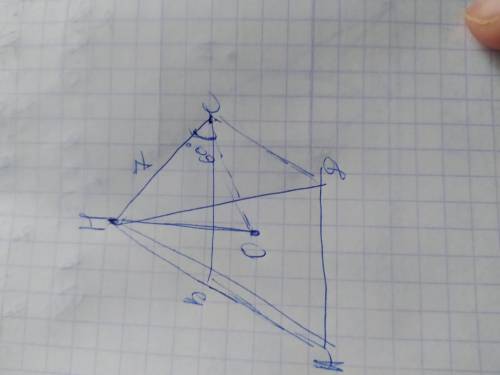
Через вершину D прямокутника ABCD проведено пряму DK, перпендикулярну до його площини. KA = 5см; KB = 7см; KC = 6см.

Знайдіть:
а) KD
б) площу прямокутника ABCD

166

366

Посмотреть ответы 1

Ответы на вопрос:

olegtab34

Геометрия

4,6(66 оценок)

ответ: (85,75√3)/3см³

Объяснение: Обозначим вершины основания пирамиды А В С Д, а её высоту НО. Проведём от точки О отрезок ОС. Высота НО образуют с проэкцией ОС прямоугольный треугольник НОС, в котором НО и ОС - катеты, а СН - гипотенуза, угол С=60°, тогда угол СНО=30°. Катет лежащий напротив него равен половине гипотенузы, поэтому ОС=НС/2=7/2=3,5см

По теореме Пифагора найдём высоту НО: НО²=НС²-ОС²=7²-(3,5)²=49-12,25=36,75; НО=√36,75=√12,25×√3=

3,5√3см

НО=3,5√3

В основе правильной четырёхугольника пирамиды лежит квадрат и если половина его диагонали ОС=3,5, тогда диагональ АС=3,5×2=7см. Так как диагональ квадрата делит его на 2 равных прямоугольных треугольника, то ∆АСД и ∆АВС- равнобедренные, потому что стороны квадрата равны, и сторона квадрата равна стороне прямоугольного треугольника. Теперь вычислим одну из сторон по формуле прямоугольного треугольника: АВ=ВС=СД=АД=АС/√2=

=7/√2см. Найдём площадь квадрата по формуле: S=(7/√2)²=

=49÷2=24,5см²

S=24,5см²

Теперь найдём объем пирамиды, зная площадь основания и высоту пирамиды по формуле: V=⅓×Sосн×h, где h- высота пирамиды:

V=⅓×24,5×3,5√3=⅓×85,75√3=

=(85,75√3)/3см³

Краткое решение:

Угол С=60°, тогда угол СНО=90-60=30°

ОС=7/2=3,5см

По теореме Пифагора НО²=НС²-ОС²=

=......3,5√3см

Диагональ АС=3,5×2=7см

∆АСД и ∆АВС равнобедренные, поэтому:

АВ=ВС=СД=АД=7/√2

Sосн=(7/√2)²=49/2=24,5см²

V=⅓×Sосн×НО=⅓×24,5×3,5√3=

=⅓×85,75√3=(85,75√3)/3см³

Боковое ребро правильной четырехугольной пирамиды равно 7 см и наклонено к плоскости основания пол у

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.