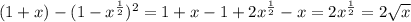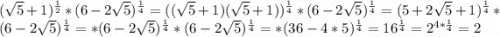В треугольнике АВС угол С равен 90°, из прямого угла проведена высота СН. Найдите sin угла HCB, если sin угла CAB = 0,4
231
377
Ответы на вопрос:
В треугольнике авс известно:
Угол С = 90°;
сн - высота;
ас = 0.8;
ан = 0.4.
Найдем sin b.
1) Рассмотрим треугольник ACH. Угол Н = 90°.
cos a = ah/ac (отношение прилежащего катета к гипотенузе);
Подставим известные значения в формулу и найдем косинус угла а.
cos a = 0.4/0.8 = 4/8 = 1/2 = 0.5;
2) Так как, cos a = sin b = AC/AB в треугольнике АВС, тогда sin b = 0.5.
В итоге получили, что синус угла b равен 0,5, то есть sin b = 0.5.
ответ: sin b = 0.5.
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
В апреле Михкель 6 раз ездил на автобусе из Тарту в Таллинн и обратно....
 лада16112.11.2021 19:39
лада16112.11.2021 19:39 -
.. 7 класс Заранее :3...
 AmeliandeAmeliande14.12.2020 17:10
AmeliandeAmeliande14.12.2020 17:10 -
1) Е 19. Укажите среди следующих множеств пустые множества: множество...
 иван205422.09.2020 07:36
иван205422.09.2020 07:36 -
(5) 8 3. Длина прямоугольника равна 96 см, что составляет 8/5 ширины....
 yroslav12020603.06.2020 06:18
yroslav12020603.06.2020 06:18 -
Подскажи , с правой стороны, составь задачу по схеме...
 89528849556keyz12.01.2022 04:48
89528849556keyz12.01.2022 04:48 -
5. Определи порядок действий и вычисли. 876 : 2 - 672 :4+ (1000...
 oksanochkabob19.07.2020 11:30
oksanochkabob19.07.2020 11:30 -
для посева заготовили семена ячменя овса проса сегодня 225000 меня...
 МаминаГадость1221.06.2023 12:28
МаминаГадость1221.06.2023 12:28 -
1) (-2.8-3.7)*3/2+6 2) 5.7-3/10*1.2+6 3) 6целых. 2/3-(-1/3)*2.5+6...
 abdulla80528.10.2020 22:13
abdulla80528.10.2020 22:13 -
До ть будь ласка! контрольна робота з літератури. потрібно здати...
 Lesha15220.05.2021 23:24
Lesha15220.05.2021 23:24 -
прямоугольник AB =4 AD=3. |AB + AD| равен: 1. 10 2. 5 3. корень7...
 5Юра111111121.03.2022 02:54
5Юра111111121.03.2022 02:54

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

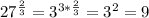 - В
- В![\frac{1}{\sqrt[5]{a^{3}} } =\frac{1}{a^{\frac{3}{5} }} =a^{-\frac{3}{5}}](/tpl/images/3965/7637/30d8a.png) - Г
- Г