Регистрация Спросить otvet5GPT
neftyanik102
27.09.2020 02:50
Математика
Есть ответ 👍

1)Запишите формулу S для вычисления площади фигуры,изображённой на рисунке. 2)Найдите площадь этой фигуры,если х=0,7 см

185
415
Посмотреть ответы 2

Ответы на вопрос:

Frolinng
Frolinng
4,8(6 оценок)

(3x*x)+(x^2)

объясняю:

мы делим эту фигуру на 2 части и у первой части выходит формула: 3x*x

а у второй части:x*x или же можно записать x^2

Злая4Пташка4
Злая4Пташка4
4,6(89 оценок)

300 см² и 200 см².

Пошаговое объяснение:

В прямом параллелепипеде боковое ребро равно 10 см, стороны основания 23 см и 11 см, диагонали основания относятся как 2: 3. Найти площади диагональных сечений.

Пусть дан прямой параллелепипед 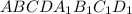ABCDA_{1} B_{1} C_{1} D_{1}.

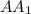AA_{1}= 10 cм, АВ = 23см, ВС =11 см. Диагонали  BD : AC =2:3.

Основанием прямой призмы является параллелограмм АВСD.

Найдем диагонали параллелограмма. По свойству квадратов диагоналей параллелограмма : сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

AC²+BD ² = 2· (AB² + BC²)

Пусть АС = 3х см, а ВD = 2х см. Тогда

(3x)² +(2x)² = 2· ( 23² +11²);

9x² +4x² =2 ·( 529 + 121);

13 x² = 2· 650;

13 x² = 1300;

x² = 1300 : 13;

x²= 100;

x= 10.

Тогда АС = 3· 10 = 30 см, ВD =2· 10 = 20 см.

Диагональное сечение - это прямоугольник, так как параллелепипед прямой.

Чтобы найти площадь прямоугольника надо длину умножить на ширину.

Прямоугольник 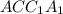ACC_{1} A_{1} - диагональное сечение

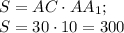S = AC \cdot AA_{1} ;\\S =30 \cdot 10 =300 см².

Прямоугольник 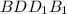BDD_{1} B_{1} - диагональное сечение

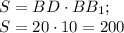S =BD \cdot BB_{1} ;\\S =20 \cdot 10 =200 см².

#SPJ1


на рисунке. Распишите

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS