Математика: Впиши подходящие достойность купюр

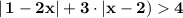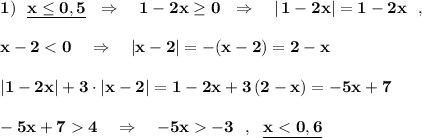
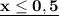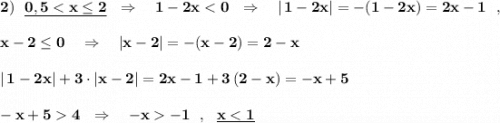
Неравенство .Модули обращаются в 0 при х=1/2 и х=2 .Эти точки разобьют числовую прямую на три промежутка . В каждом промежутке модули будут раскрываться в зависимости от знака подмодульного выражения .(1/2) (2) Рассмотрим три случая . Полученное неравенство относительно х пересекается с рассматриваемым промежутком . Поэтому на рассматриваемом промежутке решением будут . Решением будут 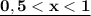. 4) Объединяем полученные решения , тогда ответ: ....

bobr528

09.11.2022 08:07

Математика

Есть ответ 👍

Впиши подходящие достойность купюр

172

318

Посмотреть ответы 1

Ответы на вопрос:

ppppppp0000

Математика

4,8(21 оценок)

Неравенство $\bf |\, 1-2x|+3\cdot |x-2) 4$ .

Модули обращаются в 0 при х=1/2 и х=2 .

Эти точки разобьют числовую прямую на три промежутка . В каждом промежутке модули будут раскрываться в зависимости от знака подмодульного выражения .

(1/2) (2)

Рассмотрим три случая .

$\bf 1)\ \ \underline{x\leq 0,5}\ \ \Rightarrow \ \ \ 1-2x\geq 0\ \ \Rightarrow \ \ \ |\, 1-2x|=1-2x\ \ ,x-2 < 0\ \ \ \Rightarrow \ \ \ |x-2|=-(x-2)=2-x|1-2x|+3\cdot |x-2|=1-2x+3\, (2-x)=-5x+7-5x+7 4\ \ \ \Rightarrow \ \ \ -5x -3\ \ ,\ \ \underline{x < 0,6}$

Полученное неравенство относительно х пересекается с рассматриваемым промежутком . Поэтому на рассматриваемом промежутке решением будут $\bf \underline{x\leq 0,5}$ .

$\bf 2)\ \ \underline{0,5 < x\leq 2}\ \ \Rightarrow \ \ \ 1-2x < 0\ \ \Rightarrow \ \ \ |\, 1-2x|=-(1-2x)=2x-1\ \ ,x-2\leq 0\ \ \ \Rightarrow \ \ \ |x-2|=-(x-2)=2-x|\, 1-2x|+3\cdot |x-2|=2x-1+3\, (2-x)=-x+5-x+5 4\ \ \Rightarrow \ \ \ -x -1\ \ ,\ \ \underline {x < 1}$

Решением будут $\bf \underline{0,5 < x < 1}$ .

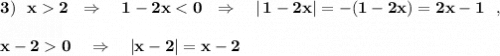
$\bf 3)\ \ x 2\ \ \Rightarrow \ \ \ 1-2x < 0\ \ \Rightarrow \ \ \ |\, 1-2x|=-(1-2x)=2x-1\ \ ,x-2 0\ \ \ \Rightarrow \ \ \ |x-2|=x-2$

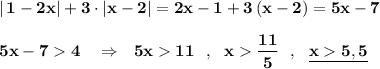
$\bf |\, 1-2x|+3\cdot |x-2|=2x-1+3\, (x-2)=5x-75x-7 4\ \ \ \Rightarrow \ \ 5x 11\ \ ,\ \ x \dfrac{11}{5}\ \ ,\ \ \underline{x 5,5}$

4) Объединяем полученные решения , тогда

$\bf x\in \underbrace{(-\infty ;0,5\ ]\cup (0,5\, ;\ 1\ )}_{(-\infty ;\, 1\, )}\cup (\, 5,5\ ;+\infty \, )\ \ \Rightarrow \ \ x\in (-\infty ;\ 1\ )\cup (\ 5,5\, ;+\infty \, )$

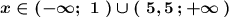ответ: $\boldsymbol{x\in (-\infty ;\ 1\ )\cup (\ 5,5\, ;+\infty \, )}$ .

|1 - 2x| + 3|x - 2| > 4 как решить поэтапно? ответ (−∞, 1) ∪ (11/5, +∞)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.