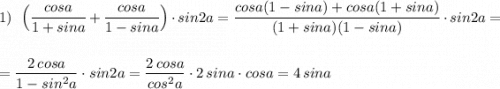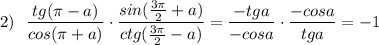dasha198156

07.04.2021 20:02

Алгебра

Есть ответ 👍

Исследуйте функцию и постройте её график:

а) y=-x^3-6x^2+36x+17 б)y=x^4+1(1/3)*x^3-24x^2+10

Подробно. Заранее

186

422

Посмотреть ответы 2

Ответы на вопрос:

lilyavenkova

Алгебра

4,7(18 оценок)

Объяснение:

ДАНО:Y(x) = x^3 -12*x² +36*x +()

ИССЛЕДОВАНИЕ.

1. Область определения D(y) = R, Х∈(-∞;+∞) - непрерывная , гладкая

2. Пересечение с осью OХ.

Разложим многочлен на множители. Y=(x-0)*(x-6)*(x-6)

Нули функции: Х₁ =0, Х₂ =6, Х₃ =6

3. Интервалы знакопостоянства.

Отрицательная - Y(x)<0 X∈(-∞;0]. Положительная -Y(x)>0 X∈[0;+∞)

4. Пересечение с осью OY. Y(0) = 0.

5. Исследование на чётность.

Y(-x) ≠ Y(x) - не чётная. Y(-x) ≠ -Y(x), Функция ни чётная, ни нечётная.

6. Первая производная. Y'(x) = 3*x² -24*x + 36 = 0

Корни Y'(x)=0. Х4=2 Х5=6

Положительная парабола - отрицательная между корнями

7. Локальные экстремумы.

Максимум Ymax(X4=2) =32. Минимум Ymin(X5=6) =0

8. Интервалы возрастания и убывания.

Возрастает Х∈(-∞;2;]U[6;+∞) , убывает - Х∈[2;6]

9. Вторая производная - Y"(x) = 6* x -24 = 0

Корень производной - точка перегиба Х₆=4

10. Выпуклая “горка» Х∈(-∞; Х₆=4]

Вогнутая – «ложка» Х∈[Х₆=4; +∞).

11. График в приложении.

Дополнительно: шаблон для описания графика.

MorficTV

Алгебра

4,8(95 оценок)

$1)\ \ \Big(\dfrac{cosa}{1+sina}+\dfrac{cosa}{1-sina}\Big)\cdot sin2a=\dfrac{cosa(1-sina)+cosa(1+sina)}{(1+sina)(1-sina)}\cdot sin2a=\\\\\\=\dfrac{2\, cosa}{1-sin^2a}\cdot sin2a=\dfrac{2\, cosa}{cos^2a}\cdot 2\, sina\cdot cosa=4\, sina$

$2)\ \ \dfrac{tg(\pi -a)}{cos(\pi+a)}\cdot \dfrac{sin(\frac{3\pi}{2}+a)}{ctg(\frac{3\pi }{2}-a)}=\dfrac{-tga}{-cosa}\cdot \dfrac{-cosa}{tga}=-1$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.