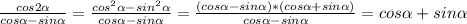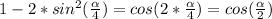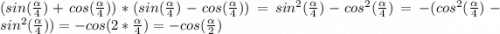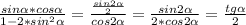Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
916. Найдите число, если: 1) 0,15 его равны 75; 2) 0,7 его равны...
 TanNam12310.01.2023 01:09
TanNam12310.01.2023 01:09 -
КРАТАКАЯ ЗАПИСЬ за 5ч пути автомобиль израсходовал 45л бензина,...
 polinaserdiuk405.12.2022 02:09
polinaserdiuk405.12.2022 02:09 -
16. В каком из примеров второе действие деление? А) 12078 +5409x50...
 34346316531320.06.2021 09:59
34346316531320.06.2021 09:59 -
клас 3. Запишите в виде неравенства и в виде числового промежутка...
 korekhova1986super01.10.2022 14:20
korekhova1986super01.10.2022 14:20 -
используя алгоритмом Дай характеристику герою царь-рыба памятка...
 lenya01314.07.2020 13:36
lenya01314.07.2020 13:36 -
Деление десятичной дроби на натуральное число. Деление десятичных...
 annshirokikh05.06.2023 22:12
annshirokikh05.06.2023 22:12 -
1) (x - 7| 0; 2) x – 4 3; 3) (2 + x| 3; 4) x + 3 2; Решите неравенства:...
 девчонка199901.09.2021 03:40
девчонка199901.09.2021 03:40 -
Б) В магазине на 3 полках стоят по 16 дисков с детскими фильма-...
 Trifonova25252521.09.2020 17:32
Trifonova25252521.09.2020 17:32 -
САМОСТОЯТЕЛЬНАЯ РАБОТА 2 Вычисли. 1% 5% 5 500 км 15% 1 200 л 900...
 qwerty112718.07.2022 03:50
qwerty112718.07.2022 03:50 -
15 РАБОТА В ГРУППЕ 7 Запиши выражения по задачам. 6) В 1984 году...
 deneleslamov201.11.2021 00:57
deneleslamov201.11.2021 00:57

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.