Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Выполните действия: а) а-b/3а + a+b/3а...
 zlooo201.05.2021 20:19
zlooo201.05.2021 20:19 -
Добрый день решить и объясните, как вы это сделали )...
 hudognik7808.03.2021 17:12
hudognik7808.03.2021 17:12 -
Вкажіть область значень функції, зображеної на малюнку...
 masha85968926.02.2020 12:56
masha85968926.02.2020 12:56 -
Свойства функции обратной пропорциональности,нужно расписать...
 тууутуууу27.02.2021 10:59
тууутуууу27.02.2021 10:59 -
Быстро Чётко по братский...
 Страус12355213.12.2021 11:13
Страус12355213.12.2021 11:13 -
А^15*а^11 а23 при а=5...
 Sanchos10611.12.2020 09:30
Sanchos10611.12.2020 09:30 -
1) 35,4 • 0,1 2) 6,25 • 0,1 3) 0,0091 : 0,001 4)4,9 • 0,001 5) 3,18 : 0,001...
 nastyluk12509.02.2021 17:39
nastyluk12509.02.2021 17:39 -
Знайдіть суму перших n натуральних чисел...
 ВанькаНер18.04.2023 08:26
ВанькаНер18.04.2023 08:26 -
Построить график функции y=3-|x|...
 anton2015b03.12.2020 06:46
anton2015b03.12.2020 06:46 -
9 і 10 розвяжіть будь ласка❤️дуже потрібно...
 ekaterinabraun523.07.2020 10:11
ekaterinabraun523.07.2020 10:11

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

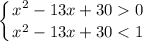
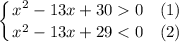
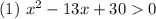
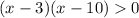
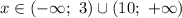
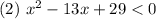
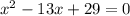
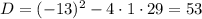
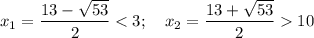
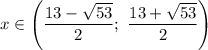
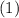 и
и