Регистрация Спросить otvet5GPT
vikysikrusinova
28.02.2020 22:58
Математика
Есть ответ 👍

Заполни таблицу.
Длина.Шир. Пер.Форм
7 см 4 см
7 см на 2 см.>
7 см на 3 см <

220
427
Посмотреть ответы 1

Ответы на вопрос:

unucozi
unucozi
4,7(13 оценок)

1.

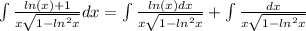
\int\limits \frac{ ln(x) + 1}{x \sqrt{1 - { ln }^{2}x } } dx = \int\limits \frac{ ln(x) dx}{x \sqrt{1 - {ln}^{2}x } } + \int\limits \frac{dx}{x \sqrt{1 - {ln}^{2} x} } \\

первый интеграл

замена:

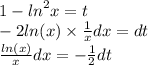
1 - {ln}^{2} x = t \\ - 2 ln(x) \times \frac{1}{x} dx = dt \\ \frac{ ln(x) }{x} dx = - \frac{1}{2} dt

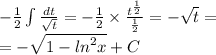
- \frac{1}{2} \int\limits \frac{dt}{ \sqrt{t} } = - \frac{1}{2} \times \frac{ {t}^{ \frac{1}{2} } }{ \frac{1}{2} } = - \sqrt{t} = \\ = - \sqrt{1 - {ln}^{2} x} + C

второй интеграл

замена:

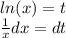
ln(x) = t \\ \frac{1}{x} dx = dt

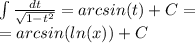
\int\limits \frac{dt}{ \sqrt{1 - {t}^{2} } } = arcsin(t) + C = \\ = arcsin( ln(x)) + C

Получаем ответ:

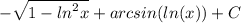
- \sqrt{1 - {ln}^{2}x } + arcsin(ln(x)) + C \\

2.

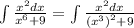
\int\limits \frac{ {x}^{2} dx}{ {x}^{6} + 9 } = \int\limits \frac{ {x}^{2} dx}{ {( {x}^{3} )}^{2} + 9 } \\

замена:

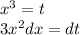
{x}^{3} =t \\ 3 {x}^{2} dx = dt

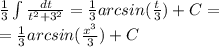
\frac{1}{3} \int\limits \frac{dt}{ {t}^{2} + {3}^{2} } = \frac{1}{3} arcsin( \frac{t}{3} ) +C = \\ = \frac{1}{3} arcsin( \frac{ {x}^{3} }{3}) + C

3.

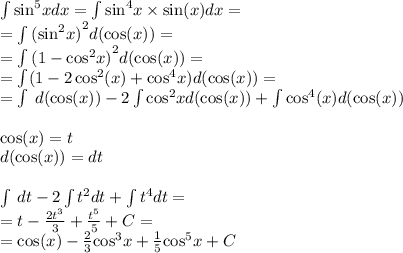
\int\limits { \sin }^{5} xdx = \int\limits { \sin }^{4} x \times \sin(x) dx = \\ = \int\limits {( { \sin }^{2}x )}^{2} d( \cos(x)) = \\ = \int\limits {(1 - { \cos }^{2}x) }^{2} d( \cos(x)) = \\ = \int\limits(1 - 2 \cos ^{2} (x) + { \cos}^{4} x)d (\cos(x)) = \\ = \int\limits \: d (\cos(x)) - 2\int\limits { \cos }^{2} x d( \cos(x)) + \int\limits \cos ^{4} (x) d (\cos(x)) \\ \\ \cos(x) = t \\ d (\cos(x)) = dt \\ \\ \int\limits \: dt - 2\int\limits {t}^{2} dt + \int\limits {t}^{4} dt = \\ = t - \frac{2 {t}^{3} }{3} + \frac{ {t}^{5} }{5} + C = \\ = \cos(x) - \frac{2}{3} { \cos }^{3} x + \frac{1}{5 } { \cos}^{5} x + C

4.

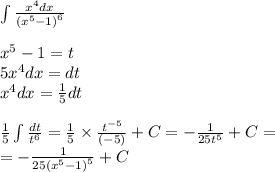
\int\limits \frac{ {x}^{4}dx }{ {( {x}^{5} - 1) }^{6} } \\ \\ {x}^{5} - 1 = t \\ 5 {x}^{4} dx = dt \\ {x}^{4} dx = \frac{1}{5} dt \\ \\ \frac{1}{5} \int\limits \frac{dt}{ {t}^{6} } = \frac{1}{5} \times \frac{ {t}^{ - 5} }{( - 5)} + C = - \frac{1}{25 {t}^{5} } + C = \\ = - \frac{1}{25 {( {x}^{5} - 1)}^{5} } + C

5.

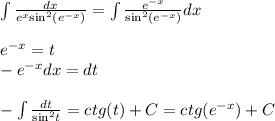
\int\limits \frac{dx}{ {e}^{x} { \sin}^{2}( {e}^{ - x}) } = \int\limits \frac{ {e}^{ - x} }{ { \sin }^{2} ( {e}^{ - x}) } dx \\ \\ {e}^{ - x} = t \\ - {e}^{ - x}dx = dt \\ \\ - \int\limits \frac{dt}{ { \sin }^{2} t} = ctg(t) + C = ctg( {e}^{ - x} ) + C

6

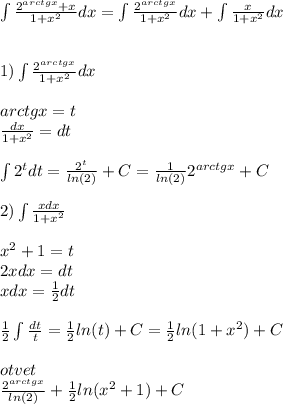
\int\limits \frac{ {2}^{arctgx} + x }{1 + {x}^{2} } dx= \int\limits \frac{ {2}^{arctgx} }{1 + {x}^{2} } dx + \int\limits\frac{x}{1 + {x}^{2} } dx \\ \\ \\ 1)\int\limits \frac{ {2}^{arctgx} }{1 + {x}^{2} } dx \\ \\ arctgx = t \\ \frac{dx}{1 + {x}^{2} } = dt \\ \\ \int\limits {2}^{t} dt = \frac{ {2}^{t} }{ ln(2) } + C = \frac{1}{ ln(2) } {2}^{arctgx} + C \\ \\ 2)\int\limits\frac{xdx}{1 + {x}^{2} } \\ \\ {x}^{2} + 1 = t \\ 2xdx = dt \\ xdx = \frac{1}{2} dt \\ \\ \frac{1}{2} \int\limits \frac{dt}{t} = \frac{1}{2} ln(t) + C = \frac{1} {2} ln(1 + {x}^{2} ) + C \\ \\ otvet \\ \frac{ {2}^{arctgx} }{ ln(2) } + \frac{1}{2} ln( {x}^{2} + 1) + C

7.

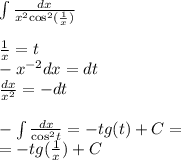
\int\limits \frac{dx}{ {x}^{2} { \cos }^{2}( \frac{1}{x} ) } \\ \\ \frac{1}{x} = t \\ - {x}^ { - 2}dx = dt \\ \frac{dx}{ {x}^{2} } = - dt \\ \\ - \int\limits \frac{dx}{ { \cos}^{2}t } = - tg(t) + C= \\ = - tg( \frac{1}{x}) + C

8.

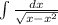
\int\limits \frac{dx}{ \sqrt{x - {x}^{2} } } \\

выделим квадрат

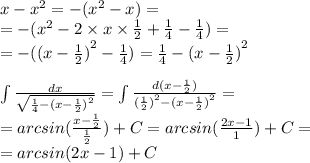
x - {x}^{2} = - ( {x}^{2} - x) = \\ = - ( {x}^{2} - 2 \times x \times \frac{1}{2} + \frac{1}{4} - \frac{1}{4} ) = \\ = - ( {(x - \frac{1}{2} )}^{2} - \frac{1}{4} ) = \frac{1}{4} - {(x - \frac{1}{2} )}^{2} \\ \\ \int\limits \frac{dx}{ \sqrt{ \frac{1}{4} - {(x - \frac{1}{2} )}^{2} } } = \int\limits \frac{d(x - \frac{1}{2} )}{ {( \frac{1}{2} )}^{2} - {(x - \frac{1}{2}) }^{2} } = \\ = arcsin( \frac{x - \frac{1}{2} }{ \frac{1}{2} } ) +C = arcsin( \frac{2x - 1}{1} ) + C= \\ = arcsin(2x - 1) + C

9.

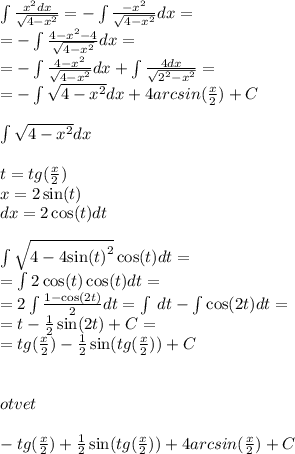
\int\limits \frac{ {x}^{2} dx}{ \sqrt{4 - {x}^{2} } } = - \int\limits \frac{ - {x}^{2} }{ \sqrt{4 - {x}^{2} } } dx = \\ = - \int\limits \frac{4 - {x}^{2} - 4 }{ \sqrt{4 - {x}^{2} } } dx = \\ = -\int\limits \frac{4 - {x}^{2} }{ \sqrt{4 - {x}^{2} } } dx + \int\limits \frac{4dx}{ \sqrt{ {2}^{2} - {x}^{2} } } = \\ = - \int\limits \sqrt{4 - {x}^{2} } dx + 4arcsin( \frac{x}{2} ) + C\\ \\ \int\limits \sqrt{4 - {x}^{2} } dx \\ \\ t = tg( \frac{x}{2}) \\ x = 2 \sin(t) \\ dx = 2 \cos(t) dt \\ \\ \int\limits \sqrt{4 - 4 { \sin(t) }^{2} } \cos(t) dt = \\ = \int\limits2 \cos(t) \cos(t) dt = \\ = 2\int\limits \frac{1 - \cos(2t) }{2} dt = \int\limits \: dt - \int\limits\cos(2t) dt = \\ = t - \frac{1}{2} \sin(2t) + C = \\ = tg( \frac{x}{2} ) - \frac{1}{2} \sin(tg( \frac{x}{2} ) ) + C \\ \\ \\o tvet \\ \\ - tg( \frac{x}{2} ) + \frac{1}{2} \sin(tg( \frac{x}{2} ) ) + 4arcsin( \frac{x}{2} ) + C

10.

\int\limits \frac{ \sin(x) }{ \sqrt{7 + 2 \cos(x) } } dx \\ \\ 2 \cos(x) + 7 = t \\ - 2 \sin(x) dx = dt \\ \sin(x) dx = - \frac{1}{2} dt \\ \\ - \frac{1}{2} \int\limits \frac{dt}{ \sqrt{t} } = - \frac{1}{2} \times \frac{ {t}^{ \frac{1} {2} } }{ \frac{1}{2} } + C = - \sqrt{t} + C= \\ = - \sqrt{7 + 2 \cos(x) } + C

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS