Анюта10072401

26.10.2022 19:35

Геометрия

Есть ответ 👍

Основание прямого параллелепипеда ромб с меньшей диагональю 12 см большая диагональ параллелепипеда равна 16 корней из 2 и образует с боковым ребром угол 45 градусов Найдите площадь полной поверхности параллелепипеда

239

416

Посмотреть ответы 2

Ответы на вопрос:

Анастасия31052006

Геометрия

4,4(52 оценок)

ответ:.......

Объяснение:

Исбанка

Геометрия

4,8(55 оценок)

Объяснение: ЗАДАНИЕ 1

Площадь шара вычисляется по формуле:

S=4πR², где R- радиус шара=13+6+8=27

S=4π×27²=4π×729=2916(ед²)

Объем шара вычисляется по формуле:

V=4/3πR³=4/3π×27³=4/3π×19683

=26244π(ед³)

ЗАДАНИЕ 2

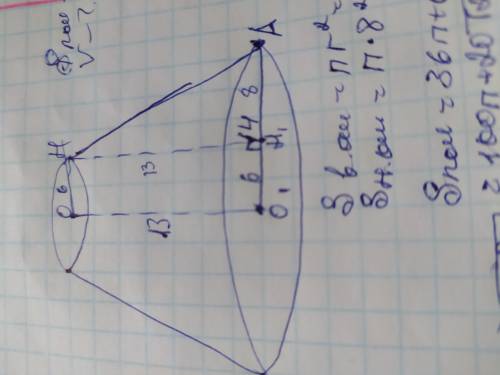
Обозначим радиусы конуса ОН и О1А. Получилась прямоугольная трапеция ОНАО1. Проведём высоту НН1 к радиусу нижнего основания О1А. Она делит О1А так, что О1А=ОН=6, значит Н1А=14-6=8.

Также получился прямоугольный треугольник НАН1, в котором радиусы основания являются катетами а образующая конуса гипотенузой. Найдём НА по теореме Пифагора:

НА²=НН1²+НА²=13²+8²=169+64=233;

НА=√233

Найдём площадь боковой поверхности конуса по формуле:

Sбок=π(R+R1)HA=π(6+14)×√233=20√233π;

√233≈15,3; 20×15,3π=306π

Найдём площадь верхнего и нижнего оснований по формуле: S=πr²

Sверх.осн=π×6²=36π

Sниж.осн=π×14²=196π

Площадь полной поверхности конуса- это сумма всех его площадей основания и боковой поверхности:

Sпол=Sбок.пов+S2хосн=306π+36π+196π==538π

Sпол=538π

Объём усечённого конуса вычисляется по формуле: V=⅓×πH(R1²+R1×R2+R2²)=

=⅓π×13(6²+6×14+14²)=13π/3(36+84+196)=

=13π/3×316=4108π/3(ед³)

или 1369π целых ⅓

ОТВЕТ: Sпол=538π(ед²); V=4108π/3(ед³)

Найти площадь полной поверхности и объём шара, радиус которого равен 13+6+8. 2. Найти площадь полной

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.