геометрия!
Задача 2. В треугольнике АВС угол А равен 100о на стороне ВС взяли точку Е и соединили с точкой А. В оба треугольника АВЕ и АСЕ вписали окружности с центрами в точках О и Q. Найти угол ОАQ

Задача 5. В треугольнике АВС АВ=АС. На стороне АС взяли точку К так, чтобы СК=СВ. Докажите, что центры окружности, вписанной в треугольник АВС совпадает с центром окружности, описанной около треугольника ВКС.

192

449

Посмотреть ответы 1

Ответы на вопрос:

Alpetrova7

Геометрия

4,6(67 оценок)

V=312√3π(см³)

Объяснение:

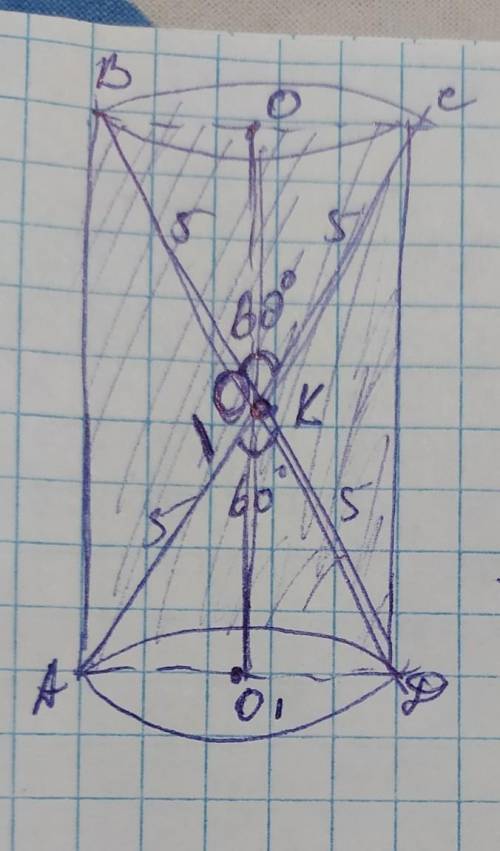
осевым сечением цилиндра является прямоугольник. Обозначим его вершины А В С Д ч диагоналями АС и ВД, точку их пересечения К, а высоту ОО1. Объем цилиндра вычисляется по формуле: V=Sосн×ОО1, где основанием является окружность. Диагонали сечения пересекаясь делятся пополам поэтому АК=КС=ВК=ВД=10÷2=5см

Рассмотрим полученный ∆АКД. Он равнобедренный и <А=<Д=(180–60)÷2=120÷2=60°

Итак: ∆АКД- равносторонний, поскольку все его углы равны, и каждый составляет 60°, поэтому АК=КД=АД=5см.

Вычислим площадь сечения АВСД по формуле:

S=сеч½×AC²×sin60°=½×10²×√3/2=½×100×√3/2=

=25√3см²

Sсеч=25√3см²

Зная площадь сечения найдём высоту ОО1:

ОО1=Sсеч÷АД=25√3÷5=5√3см; ОО1=5√3см

Радиус АО1=О1Д=АД÷2=5÷2=2,5 см

Sосн=πr²=π×(2,5)²=6,25π

Теперь найдём объем цилиндра зная его площадь основания и высоту:

V=Sосн×ОО1=6,25π×5√3=312√3π(см³)

діагональ осьового перерізу циліндра має довжину 10 см, а кут між його діагоналями 60 градусів. Знай

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.