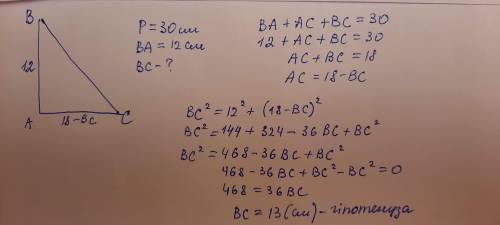Основние пирамиды — прямоугольник ABCD, AB=18 м, BC=18 м, высота пирамиды проходит через точку пересечения диагоналей основания и равна 12 м. Найдите площадь полной поверхности пирамиды.

173

339

Посмотреть ответы 2

Ответы на вопрос:

chiminswife

Геометрия

4,4(33 оценок)

Пирамида MABCD, основание - прямоугольник ABCD: AD=BC=18 см; AB=CD=10 см; O- точка пересечения диагоналей AС и BD, MO - высота пирамиды. Так как у прямоугольника диагонали равны и точкой пересечения делятся пополам, то OA = OB = OC = OD - это проекции боковых ребер на основание. Проекции наклонных равны, следовательно, наклонные тоже равны : AM = BM = CM = DM - боковые ребра пирамиды. Тогда ΔAMD = ΔBMC - по трём равным сторонам, ΔAMB = ΔDMC - по трём равным сторонам. Проведем KT║AD ⇒ OK=OT=AD/2 = 18/2 = 9 смΔMOT - прямоугольный, теорема ПифагораMT² = MO² OT² = 12² 9² = 144 81=225 = 15²MT = 15 см см²Проведем FG║DC ⇒ OG=OF=DC/2 = 10/2 = 5 смΔMOF - прямоугольный, теорема ПифагораMF² = MO² OF² = 12² 5² = 144 25 = 169 = 13²MF = 13 см см²Площадь боковой поверхности пирамиды см²Sбок = 384 см²Площадь основания см²Площадь полной поверхности пирамиды S = 384 180 = 564 см²

tanzbis

Геометрия

4,7(55 оценок)

Відповідь: 13 см

Пояснення: використовучи периметр трикутника, визначаємо АС.

Далі обраховуємо рівняння, використовуючи теорему Піфагора.

Скидую фото.

периметр трикутника дорівнює 30 см, а один з його катетів-12см. знайдіть (у см) гіпотенузу трикутник

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.