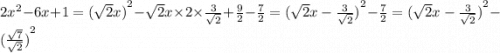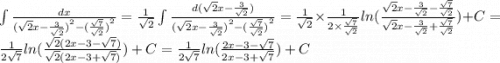Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Решить эти 3 задачи, очень кто может Решить эти 3 задачи, очень...
 никич4322.10.2021 19:15
никич4322.10.2021 19:15 -
Между числами 8 и (-1) вставьте два числа, чтобы они, вместе...
 Daniljj115.04.2023 23:59
Daniljj115.04.2023 23:59 -
Группу из 30 студентов нужно разделить, на 4 бригады, причем...
 Агентс20.05.2023 01:28
Агентс20.05.2023 01:28 -
Игорь закрасил (n – 1) клетку в таблице n x n. После этого он...
 serhio200008.06.2020 14:12
serhio200008.06.2020 14:12 -
Для функции 4+соs x найдите первообразную, график которой проходит...
 Сас11105.03.2021 07:36
Сас11105.03.2021 07:36 -
Завод выпускает детали, собранные в 2 разных цехах. Известно,...
 LilGirl107.03.2022 01:56
LilGirl107.03.2022 01:56 -
3)Тіло рухається прямолінійно за законом S(t)= t^2-4t+186. Знайти...
 АринаВарданян03.05.2020 10:15
АринаВарданян03.05.2020 10:15 -
решить уравнения решить уравнения >...
 mslogvineko07.02.2021 08:20
mslogvineko07.02.2021 08:20 -
Даны комплексные числа Z1= 2-3і ; Z2= 2+3і. Найдите Z 1^2-2...
 Cepёжka26.01.2021 10:51
Cepёжka26.01.2021 10:51 -
А)найдите координаты точек пересечения графика линейного уравнения...
 danisdigger05.06.2022 18:04
danisdigger05.06.2022 18:04

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.