Найдите радиус окружности, вписанной в прямоугольную трапецию, если основания трапеции равны 3 и

229

410

Посмотреть ответы 1

Ответы на вопрос:

Comalia

Геометрия

4,4(49 оценок)

Средняя линия трапеции равна 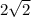$2\sqrt 2$ ;

площадь трапеции равна 4

Объяснение:

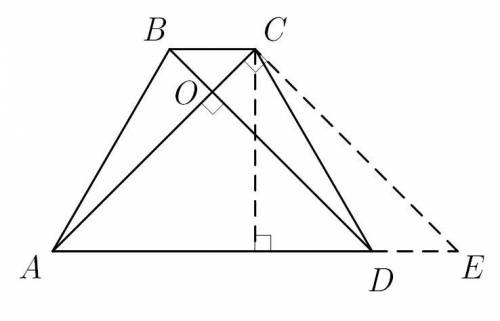
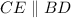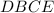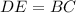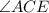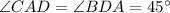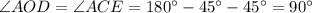Проведем $CE\parallel BD$ . Тогда четырехугольник DBCE параллелограмм, DE = BC , $\angle ACE$ — угол между диагоналями. Так как $\angle CAD = \angle BDA = 45^\circ$ , то $\angle AOD = \angle ACE = 180^\circ - 45^\circ - 45^\circ = 90^\circ$ .

В треугольнике 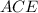ACE по теореме Пифагора

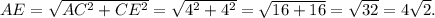
$AE = \sqrt {A{C^2} + C{E^2}} = \sqrt {{4^2} + {4^2}} = \sqrt {16 + 16} = \sqrt {32} = 4\sqrt 2 .$

Но 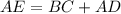AE = BC + AD , тогда средняя линия трапеции

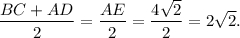
$\displaystyle\frac{{BC + AD}}{2} = \displaystyle\frac{{AE}}{2} = \displaystyle\frac{{4\sqrt 2 }}{2} = 2\sqrt 2 .$

Найдем высоту 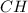прямоугольного треугольника 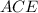ACE (она же и высота трапеции) по формуле

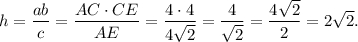
$h = \displaystyle\frac{{ab}}{c} = \displaystyle\frac{{AC \cdot CE}}{{AE}} = \displaystyle\frac{{4 \cdot 4}}{{4\sqrt 2 }} = \displaystyle\frac{4}{{\sqrt 2 }} = \displaystyle\frac{{4\sqrt 2 }}{2} = 2\sqrt 2 .$

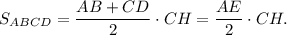
${S_{ABCD}} = \displaystyle\frac{{AB + CD}}{2} \cdot CH = \displaystyle\frac{{AE}}{2} \cdot CH.$

Значит

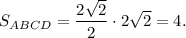
${S_{ABCD}} = \displaystyle\frac{{2\sqrt 2 }}{2} \cdot 2\sqrt 2 = 4.$

У равнобедренной трапеции диагональ 4см и с большой основой составляет 45 градусный угол. Найти сред

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.