Четырёхугольник ABCD задан координатами своих вершин A (2; 5), B (–3; 7), C (–6; 2), D (–1; –1). Выполните построения и укажите координаты вершин четырёхугольника A1B1C1D1, полученного путём параллельного переноса на вектор a{3,-2} из четырёхугольника ABCD. ответ: А1 ( ; ), В1 ( ; ), С1 ( ; ), D1

Объяснение:

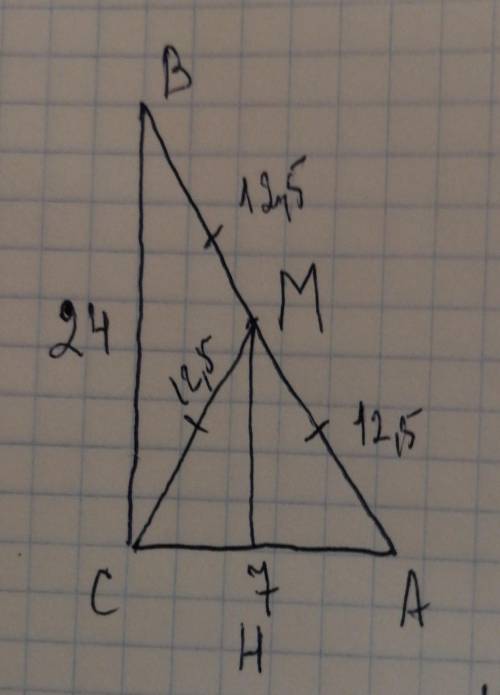
По теореме Пифагора :

АВ=корень (ВС^2-АС^2)=

корень (24^2-7^2)=корень (576+49)=

=корень 625=25 см

Медиана, проведённая из вершины прямого угла равна половине гипотенузы :

СМ=1/2×АВ=1/2×25=25/2=12,5 см

Острый угол между гипотенузой и медианой

это угол СМА, т. к против меньшей стороны лежит меньший угол (у тр-ков ВСМ и СМА боковые стороны равны, а сторона АС меньше стороны ВС, значит <СМА меньший)

Тр-к СМА - равнобедренный (СМ=АМ),

МН - высота и медиана.

АН=АС:2=7:2=3,5 см

Тр-к НМА - прямоугольный,

По теореме Пифагора :

МН=корень (АМ^2-АН^2) =

=корень (12,5^2-3,5^2)=корень 144=12 см

S=1/2×AC×MH=1/2×7×12=42 cм^2

S=1/2×CM×AM×sin<CMA=

=1/2×12,5×12,5×sin<CMA

42=78,125×sin<CMA

sin<CMA=42:78,125=0,5376

По теореме косинусов :

cos<CMA=(CM^2+AM^2-AC^2)/(2×CM×AM) =

=(12,5^2+12,5^2-7^2)/(2×12,5×12,5)=

=(156,25+156,25-49)/312,5=

=263,5/312,5=0,8432

ответ : sin<CMA=0,5376

cos<CMA=0,5376