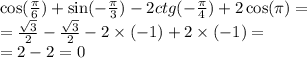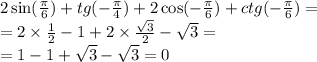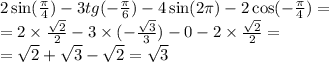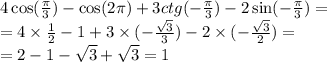Найди значение аргумента x, при котором функция y=4x принимает заданное значение, равное 64.
106
234
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Найди значение a по графику функции y=ax²+bx+c, представленному на рисунке....
 kiki000412.11.2022 20:57
kiki000412.11.2022 20:57 -
Задайте линейную функцию у = кх формулой, если известно, что ее график параллелен...
 3asyavasilkova325.09.2020 07:24
3asyavasilkova325.09.2020 07:24 -
Является ли решением уравнения 3х+2у-8=0 пара чисел (1;2)? Можете расписать...
 zwezdael30.09.2020 01:21
zwezdael30.09.2020 01:21 -
с вынесением общего множителя за скобки...
 andreewnamap0c5nx19.07.2020 21:41
andreewnamap0c5nx19.07.2020 21:41 -
1. У выражение. а) 4b (2 + b) – (b – 3) (b + 4); в) 30y + 2 (y – 5)2. б)...
 Sharjnik22.08.2022 03:10
Sharjnik22.08.2022 03:10 -
Сократи алгебраическую дробь 18⋅a1112⋅a3. Выбери, в каком виде должен быть...
 farid2008farid13.01.2020 16:20
farid2008farid13.01.2020 16:20 -
Решить номера: 31.10 и 31.11 на фото: )...
 chudmaev200301.01.2022 07:20
chudmaev200301.01.2022 07:20 -
Не игнорьте ! «формула сокращённого умножения « a в 2степ.-в в2степ. = (а-в)(а+в)....
 BabaShyra03.01.2023 13:35
BabaShyra03.01.2023 13:35 -
Піднесіть многочлен до степеня 3x+2y^4. порахуйте для значень x=1, y=2....
 g11666330.06.2023 18:40
g11666330.06.2023 18:40 -
Расстояние между двумя пристанями катер прошёл по течению реки за 7 часов...
 MadiHale26.04.2022 07:24
MadiHale26.04.2022 07:24

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.