Регистрация Спросить otvet5GPT
Раммроль
18.10.2020 02:33
Геометрия
Есть ответ 👍

Уколо вписано правильний шестикутник, сторона якого дорівнює а. знайдіть сторону трикутника, описаного навколо цього кола.

243
464
Посмотреть ответы 1

Ответы на вопрос:

toshakalashnik
toshakalashnik
4,5(58 оценок)

№1. Параллельность прямых a и b доказана.

№2. Параллельные прямые а и с.

Объяснение:

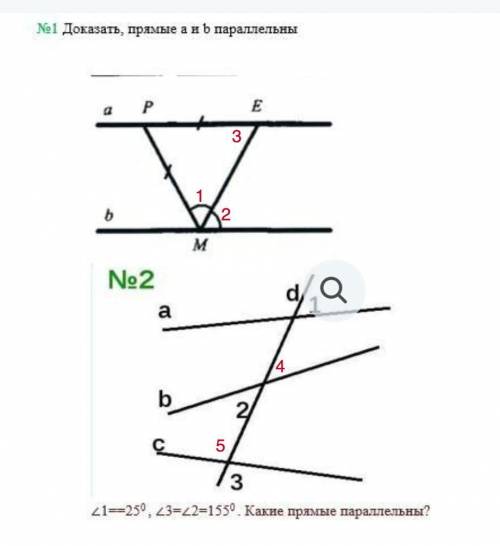
№1

Надо доказать параллельность прямых а и b.

Дано: прямые а и b.

MP = PE;

МР и МЕ - секущие;

∠1 = ∠2;

Доказать: a || b.

Доказательство:

Для того, чтобы доказать параллельность прямых  a и b, надо доказать один из признаков параллельности прямых.

1. Рассмотрим ΔМРЕ.

МР =  РЕ (по условию)

⇒ ΔМРЕ - равнобедренный.

Углы при основании равнобедренного треугольника равны.

⇒ ∠1 = ∠3

   ∠1 = ∠2 (условие)

⇒ ∠2 = ∠3 - накрест лежащие при a и b и секущей МЕ.

Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

⇒ a || b.

№2.

Найти параллельные прямые.

Дано: прямые a, b, c.

d - секущая;

∠1 = 25°; ∠2 = ∠3 = 155°.

Найти: параллельные прямые.

1) ∠3 = ∠5 (вертикальные)

  ∠3 = ∠2 = 155° (условие)

⇒ ∠5 = ∠2 = 155°.

2) ∠2 и ∠5 - внутренние односторонние.

Если при пересечении двух прямых секущей, сумма внутренних односторонних углов равна 180°, то прямые параллельны.

Проверим:

∠1 + ∠5 = 155°+ 155° = 310° ≠ 180°

⇒ прямые c и b НЕ параллельны, так как признак параллельности не соблюдается.

3) ∠2 = ∠4 = 155° (вертикальные)

4) ∠4 и ∠1 - соответственные.

∠4 = 155° (п.3)

∠1 = 25° (условие)

Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

∠1 ≠ ∠4 ⇒ прямые а и b НЕ параллельны.

5) Проверим параллельность а и с.

∠1 = 25°; ∠3 = 155° (условие)

6) ∠1 и ∠3 - внешние односторонние.

Если при пересечении двух прямых секущей, сумма внешних односторонних углов равна 180°, то прямые параллельны.

Проверим:

∠1 + ∠2 = 25° + 155° = 180°

⇒ прямые а и с - параллельны.


РЕШИТЬ 2 ЗАДАЧИ, БУДУ ОЧЕНЬ БЛАГОДАРНА, задания в файле

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS