Регистрация Спросить otvet5GPT
satova1
16.12.2021 20:24
Математика
Есть ответ 👍

Доказать что для произвольных чисел a b c d справедливо неравенство

1/a+2/b+8/c+16/d больше или равно 64/(a+b+c+d)

249
257
Посмотреть ответы 3

Ответы на вопрос:

natakleymyk
natakleymyk
4,4(57 оценок)

Решение : ////////////////////////////////////////////////

Angelina23411
Angelina23411
4,6(26 оценок)

Должно быть a>0, b>0, c>0, d>0, а так же 1/a+1/b+4/c+16/d≥64/(a+b+c+d)

Пошаговое объяснение:

1/a+2/b+8/c+16/d≥64/(a+b+c+d)⇔(a+b+c+d)(1/a+2/b+8/c+16/d)≥64

Докажем последнее неравенство используя неравенство Коши-Буняковского

(a₁²+a₂²+a₃²+...+aₓ²)(b₁²+b₂²+b₃²+...+bₓ²)≥(a₁b₁+a₂b₂+a₃b₃+...+aₓbₓ)²

(a+b+c+d)(1/a+2/b+8/c+16/d)=

=((√a)²+(√b)²+(√c)²+(√d)²)((1/√a)²+(√(2/b))²+(√(8/c))²+(√(16/d))²)≥

(√a·1/√a+√b·√2/b+√c√(8/c)+(√d√(16/d))²=(√1+√2+√8+√16)=(5+3√2)²>

>(5+3√1,96)²=(5+3·1,4)²=9,2²=84,64⇒(a+b+c+d)(1/a+2/b+8/c+16/d)>64

Доказано, что (a+b+c+d)(1/a+2/b+8/c+16/d)>64⇒

⇒1/a+2/b+8/c+16/d>64/(a+b+c+d)

Valentinka14485
Valentinka14485
4,4(100 оценок)

2.19: 1) 2; 2)1

2.21: 1) {0;1}; 2) 2

Пошаговое объяснение:

2.19.

1)

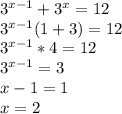
3^{x-1} + 3^x = 12\\3^{x-1}(1 + 3) = 12\\3^{x-1}*4 = 12\\3^{x-1} = 3\\x - 1 = 1\\x = 2

ответ: 2

2)

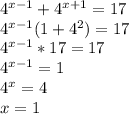
4^{x-1} + 4^{x+1} = 17\\4^{x-1}(1 + 4^2) = 17\\4^{x-1} * 17 = 17\\4^{x-1} = 1\\4^x = 4\\x = 1

ответ: 1

2.21

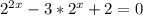
1) 2^{2x} - 3 * 2^x + 2 = 0

Сделаем замену 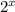2^x = y

Получаем квадратное уравнение:

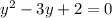
y^2 - 3y + 2 = 0

Решив его, получаем 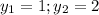y_1 = 1; y_2 = 2

При y = 1,

2^x = 1\\x = 0

При y = 2,

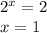
2^x = 2\\x = 1

ответ: 0; 1

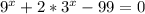
2) 9^x + 2 * 3^x - 99 = 0

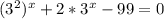
(3^2)^x + 2 * 3^x - 99 = 0

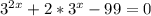
3^{2x} + 2 * 3^x - 99 = 0

Сделаем замену 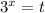3^x = t

Получаем квадратное уравнение:

t^2 + 2t - 99 = 0

Решая его, получаем 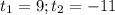t_1 = 9; t_2 = -11

При t = 9:

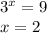
3^x = 9\\x = 2

При t = -11:

3^x = -11

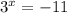
Решений нет при t = -11

ответ: 2

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS