Геометрия: Геометрия подробно !!!!!!!!!!!!!!!

Кирилл222123123413

21.09.2022 18:11

Геометрия

Есть ответ 👍

Геометрия подробно !!!!!!!!!!!!!!!

284

288

Посмотреть ответы 1

Ответы на вопрос:

Samvel7777

Геометрия

4,6(97 оценок)

Объяснение:

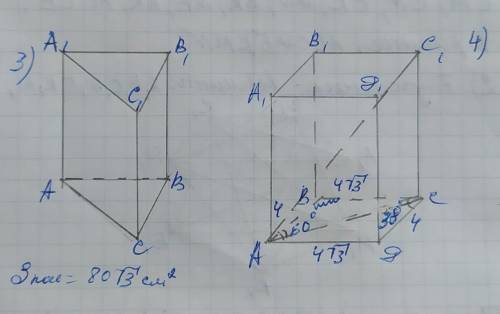
№3

Обозначим вершины призмы АВСА₁В₁С₁. Так как призма правильная, то в её основании лежит равносторонний треугольник, поэтому АВ=ВС=АС, а также все боковые грани равны между собой и поскольку площадь основания равна площади одной из боковых граней, то все грани призмы будут равновеликими, и так как граней 5 (3 боковых и 2 грани основания), то площадь каждой грани, а также площадь основания составят:

Sгр.=80√3÷5=16√3(см²).

По формуле площади равностороннего треугольника найдём сторону основания:

$\\ \\ s = \frac{a {}^{2} \sqrt{3} }{4}$

где а – сторона треугольника, в нашем случае основания. Перемножим крест накрест:

а²√3=4S

a²√3=4×16√3

a²√3=64√3

a²=64√3÷√3

a²=64

a=√64

a=8(см) – сторона основания

Узнаем высоту призмы АА₁:

АА₁=ВВ₁=СС₁=S÷AC=16√3÷8=2√3(см)

Найдём объем призмы по формуле:

V=Sосн.×АА₁=16√3×2√3=32×3=96(см³)

ОТВЕТ: V=96(см³)

№4

Обозначим вершины призмы АВСДА₁В₁С₁С₁Д₁.

Найдём площадь основания АВСД по формуле:

Sосн=ВС×СД×sinC=4√3×4×sin30°=

=16√3×1/2=8√3(см²).

Сумма углов параллелограмма, прилегающих к одной стороне равна 180°, поэтому ∠В=∠Д=180–∠С=180–30=150°.

Проведём в основании диагональ АС и рассмотрим ∆АВС и найдём АС по теореме косинусов:

АС²=АВ²+ВС²–2×АВ×АС×cos150°=

=4²+(4√3)²–2×4×4√3×(–√3/2)=

=16+16×3+16√3×√3=16+48+16×3=64+48=112АС=√112=4√7(см).

Найдём через тангенс угла высоту СС₁:

СС₁=АС×tg60°=4√7×√3=4√21(см)

V=Sосн×СС₁=8√3×4√21=32√3×√21=

=32√63=32×3√7=96√7(см³)

ОТВЕТ: V=96√7(см³)

с геометрией Нужно 3 и 4 задача с рисунками

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.