domnet

11.09.2020 20:26

Есть ответ 👍

Дано : прямоугольный параллелепипед.
a = 30 см
c - ? в 3 р < чем a
b - ? на 5 см > чем c
найти : v (объём) прямоугольного параллелепипеда.

277

466

Посмотреть ответы 3

Ответы на вопрос:

xasiyeva82p0c95p

Математика

4,4(76 оценок)

ответ:

с=10

b=15

v=4500cm²

пошаговое объяснение:

c=30: 3=10cm

b=10+5=15cm

v=10*15*30=4500cm²

morgo19

Математика

4,8(25 оценок)

ответ: 4500 см^3

пошаговое объяснение:

30: 3=10(см)-с

10+5=15(см)-b

v=abc=30*15*10=4500(cм^3)

ооиррррр

Математика

4,5(53 оценок)

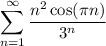$\displaystyle \sum_{n=1}^{ \infty} \dfrac{n^{2}\cos (\pi n)}{3^{n}}$ — знакочередующийся ряд, поскольку функция косинус при различных 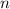является знакопеременной.

1) Находим ряд из абсолютных величин:

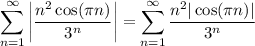$\displaystyle \sum_{n=1}^{ \infty} \left| \dfrac{n^{2}\cos (\pi n)}{3^{n}} \right| = \sum_{n=1}^{ \infty} \dfrac{n^{2}| \cos (\pi n)|}{3^{n}}$ — знакоположительный числовой ряд

2) Исследуем ряд на сходимость.

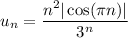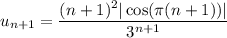
Здесь $\displaystyle u_{n} = \dfrac{n^{2}| \cos (\pi n) | }{3^{n}}$ и $\displaystyle u_{n+1} = \dfrac{(n+1)^{2}| \cos (\pi (n+1)) | }{3^{n+1}}$

Находим предел:

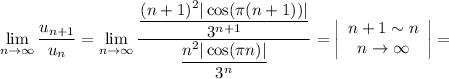
$\displaystyle \lim_{n \to \infty} \dfrac{u_{n+1}}{u_{n}} = \lim_{n \to \infty} \dfrac{ \dfrac{(n+1)^{2}| \cos (\pi (n+1)) | }{3^{n+1}}}{\dfrac{n^{2}| \cos (\pi n) | }{3^{n}}} = \left|\begin{array}{ccc}n + 1 \sim n\\n \to \infty \\\end{array}\right| =$

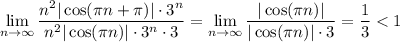
$\displaystyle \lim_{n \to \infty} \dfrac{n^{2}|\cos (\pi n + \pi)| \cdot 3^{n}}{n^{2}|\cos (\pi n)| \cdot 3^{n} \cdot 3} = \lim_{n \to \infty} \dfrac{|\cos (\pi n)|}{|\cos (\pi n)| \cdot 3} = \dfrac{1}{3} < 1$

По признаку Даламбера ряд из абсолютных величин 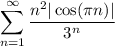$\displaystyle \sum_{n=1}^{ \infty} \dfrac{n^{2}| \cos (\pi n)|}{3^{n}}$ расходится.

3) Теорема Лейбница:

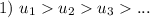
$1) \ u_{1} u_{2} u_{3} ...$

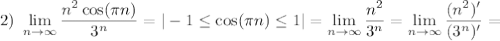
$2) \ \displaystyle \lim_{n \to \infty} \dfrac{n^{2}\cos (\pi n)}{3^{n}} = |-1 \leq \cos(\pi n) \leq 1| = \lim_{n \to \infty} \dfrac{n^{2}}{3^{n}} = \lim_{n \to \infty} \dfrac{(n^{2})'}{(3^{n})'} =$

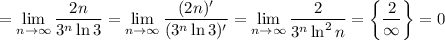
$\displaystyle = \lim_{n \to \infty} \dfrac{2n}{3^{n} \ln 3} = \lim_{n \to \infty} \dfrac{(2n)'}{(3^{n} \ln 3)'} = \lim_{n \to \infty} \dfrac{2}{3^{n}\ln^{2}n} = \left\{\dfrac{2}{\infty} \right\} = 0$

Условия выполнены, значит, знакочередующийся ряд 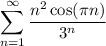$\displaystyle \sum_{n=1}^{ \infty} \dfrac{n^{2}\cos (\pi n)}{3^{n}}$ является условно сходящимся.

ответ: условно сходящийся.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.