Регистрация Спросить otvet5GPT
zali8
17.06.2022 17:53
Алгебра
Есть ответ 👍

Найти область значения функции, заданной формулой : f (x) =x²+1
убедительная просьба: если не знаете - не беритесь

191
368
Посмотреть ответы 3

Ответы на вопрос:

хотам3
хотам3
4,6(75 оценок)

ответ:

объяснение:

f (x) =x²+1

0≤x²< +∞ так как квадрат любого числа неотрицателен. прибавляя к обеим частям 1, получаем

1≤x²+1< +∞

ответ: f (x)∈[1; +∞)

солнвшко
солнвшко
4,5(86 оценок)

ответ:

е(у)=[1; +бесконечности)

объяснение:

х^2≥0

следовательно,

х^2+1≥1

то есть е(у)=[1; +бесконечности)

evbarseguan
evbarseguan
4,6(39 оценок)

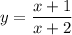
y=\dfrac{x+1}{x+2}

Составим уравнение касательной к графику функции в точке 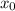x_0:

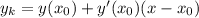
y_k=y(x_0)+y'(x_0)(x-x_0)

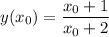
y(x_0)=\dfrac{x_0+1}{x_0+2}

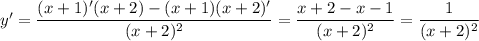
y'=\dfrac{(x+1)'(x+2)-(x+1)(x+2)'}{(x+2)^2}=\dfrac{x+2-x-1}{(x+2)^2}=\dfrac{1}{(x+2)^2}

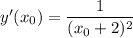
y'(x_0)=\dfrac{1}{(x_0+2)^2}

Уравнение касательной:

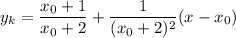
y_k=\dfrac{x_0+1}{x_0+2}+\dfrac{1}{(x_0+2)^2}(x-x_0)

Преобразуем уравнение:

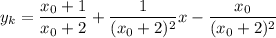
y_k=\dfrac{x_0+1}{x_0+2}+\dfrac{1}{(x_0+2)^2}x-\dfrac{x_0}{(x_0+2)^2}

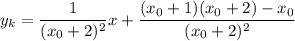
y_k=\dfrac{1}{(x_0+2)^2}x+\dfrac{(x_0+1)(x_0+2)-x_0}{(x_0+2)^2}

y_k=\dfrac{1}{(x_0+2)^2}x+\dfrac{x_0^2+2x_0+2}{(x_0+2)^2}

Так как касательная параллельная прямой y= x + 5, то угловые коэффициенты этих прямых равны:

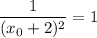
\dfrac{1}{(x_0+2)^2}=1

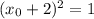
(x_0+2)^2=1

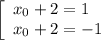
\left[\begin{array}{l} x_0+2=1\\ x_0+2=-1\end{array}

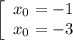
\left[\begin{array}{l} x_0=-1\\ x_0=-3\end{array}

Проверим, какие касательные получаются в каждом из двух случаев.

При 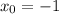x_0=-1:

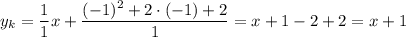
y_k=\dfrac{1}{1}x+\dfrac{(-1)^2+2\cdot(-1)+2}{1}=x+1-2+2=x+1

Касательная параллельная заданной по условию прямой y=x+5.

При x_0=-3:

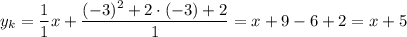
y_k=\dfrac{1}{1}x+\dfrac{(-3)^2+2\cdot(-3)+2}{1}=x+9-6+2=x+5

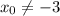Заметим, что в этом случае касательная совпадает с заданной по условию прямой y=x+5. Значит, x_0\neq -3.

Таким образом, условию удовлетворяет единственное значение 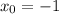x_0=-1.

ответ: -1

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS