Регистрация Спросить otvet5GPT
sagynnn
06.05.2020 05:12
Алгебра
Есть ответ 👍

Исследуйте на монотонность y=2x^2-3; y=x^2+2x​

185
209
Посмотреть ответы 3

Ответы на вопрос:

sanekakot
sanekakot
4,4(46 оценок)

ответ:

y = e^{x} * (3x -2)

y' = e^{x} * (3x - 2) + 3 * e^{x} = 3x * e^{x} - 2 * e^{x} + 3 * e^{x} = 3x * e^{x} + e^{x}

3x * e^{x} + e^{x} = 0  

3x * e^{x} = - e^{x}  

x = - \frac{1}{3}

функция убывает на промежутке ( - бесконечность ; -1/3)

возрастает (- 1/3 ; + бесконечность)

точка минимума х = - 1/3 ;  

y(-\frac{1}{3}) = e^{-\frac{1}{3} }* (3 * (-\frac{1}{3}) - 2) = e^{3} * (-3) = -3 * e^{3}

min(-1/3 ; -3*e^{3})

объяснение:

AnonimkaNya
AnonimkaNya
4,4(79 оценок)

ответ:

объяснение: y = e^{x} * (3x -2)

y' = e^{x} * (3x - 2) + 3 * e^{x} = 3x * e^{x} - 2 * e^{x} + 3 * e^{x} = 3x * e^{x} + e^{x}

3x * e^{x} + e^{x} = 0  

3x * e^{x} = - e^{x}  

x = - \frac{1}{3}

функция убывает на промежутке ( - бесконечность ; -1/3)

возрастает (- 1/3 ; + бесконечность)

точка минимума х = - 1/3 ;  

y(-\frac{1}{3}) = e^{-\frac{1}{3} }* (3 * (-\frac{1}{3}) - 2) = e^{3} * (-3) = -3 * e^{3}

min(-1/3 ; -3*e^{3})

подробнее - на -

LoveSmile7890
LoveSmile7890
4,5(62 оценок)

x₁=16; x₂=9.

Объяснение:

CD⊥AD - касательная и радиус проведённый в точку соприкосновения. AE=AD - радиусы первой окружности.

ΔACD~ΔCBD - по двум углам.

∠CAD=∠BCD и ∠ADC=90°=∠CDB ⇒ 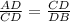\frac{AD}{CD} =\frac{CD}{DB}

AD×DB = CD²=12².

Пусть тогда:

AD=x, то DB =AB-AD=25-x.  

x×(25-x) = 144;  

x²-25x+144=0;  

x(x-16)-9(x-16)=0;  

(x-16)(x-9)=0

x₁=16; x₂=9.  

ответ: x₁=16; x₂=9.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS