Боковая поверхность конуса равна 100 пи см2, образующая равна 20, найти высоту?

290

382

Посмотреть ответы 1

Ответы на вопрос:

эмирия

Математика

4,5(96 оценок)

Пошаговое объяснение:

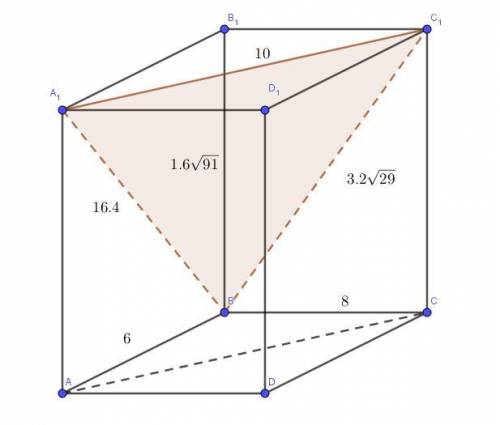
Найдем данное сечение:

Соединим точки BA₁, так как сечение проходит через прямую BA₁.

По условию, наше сечение параллельно АС, значит в этой плоскости должна найтись такая прямая, которая будет параллельна АС.

Для этого проведем отрезок из точки A₁ до С₁, ведь А₁С₁║AC.

Соединим точки В и С₁, так как они лежат в одной плоскости ВВ₁С₁.

ΔА₁ВС₁ - искомое сечение.

Все 3 измерения нашего параллелепипеда известны, поэтому находим стороны треугольника по теореме Пифагора:

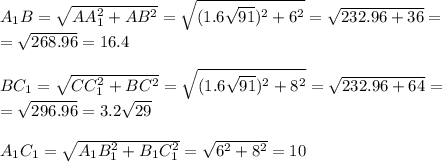
$A_1B=\sqrt{AA_1^2+AB^2} =\sqrt{(1.6\sqrt{91} )^2+6^2} =\sqrt{232.96+36}= \\ =\sqrt{268.96}= 16.4 \\ \\ BC_1=\sqrt{CC_1^2+BC^2} =\sqrt{(1.6\sqrt{91} )^2+8^2} =\sqrt{232.96+64}= \\ =\sqrt{296.96}= 3.2\sqrt{29} \\ \\ A_1C_1=\sqrt{A_1B_1^2+B_1C_1^2}= \sqrt{6^2+8^2}=10$

Площадь искомого треугольника найдем по формуле Герона:

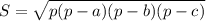
$S=\sqrt{p(p-a)(p-b)(p-c)}$

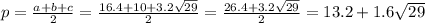
$p=\frac{a+b+c}{2}=\frac{16.4+10+3.2\sqrt{29} }{2} =\frac{26.4+3.2\sqrt{29} }{2} =13.2+1.6\sqrt{29}$

$S=\sqrt{(13.2+1.6\sqrt{29})(13.2+1.6\sqrt{29}-16.4)(13.2+1.6\sqrt{29}-10)(13.2+1.6\sqrt{29}-3.2\sqrt{29})} \\ =\sqrt{(13.2+1.6\sqrt{29})(1.6\sqrt{29}-3.2)(3.2+1.6\sqrt{29})(13.2-1.6\sqrt{29})}= \\= \sqrt{(13.2+1.6\sqrt{29})(13.2-1.6\sqrt{29})(1.6\sqrt{29}-3.2)(1.6\sqrt{29}+3.2)}= \\\sqrt{(13.2^2-(1.6\sqrt{29})^2)((1.6\sqrt{29})^2-3.2^2)}= \sqrt{(174.24-74.24)(74.24-10.24)} = \\ =\sqrt{100*64}=10*8=80$

Задачка на стереометрию, ответ отмечен, мне нужно объснение

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.