Регистрация Спросить otvet5GPT
arishaprohorenk
20.01.2022 18:23
Геометрия
Есть ответ 👍

Напишите признаки и свойства трапеций равнобедреннойи прямоугольной ,

191
449
Посмотреть ответы 2

Ответы на вопрос:

Aysun115
Aysun115
4,4(81 оценок)
Свойства и признаки равнобедренной трапеции - трапеция является равнобедренной тогда и только тогда, когда углы при ее основании равны (диагонали равны)трапецияопределение: трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие не параллельны.параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. отрезок, соединяющий середины боковых сторон, называется средней линией.определение: трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны.определение: трапеция, один из углов которой прямой, называется прямоугольной.свойства трапеции: ее средняя линия параллельна основаниям и равна их полусумме;   если трапеция равнобокая, то ее диагонали равны и углы при основании равны;   признаки трапеции: четырёхугольник является трапецией, если его параллельные стороны не равныформулы площади: a и b — основания; h — расстояние между ними; l — средняя линия.s = lh
kpy4
kpy4
4,4(87 оценок)

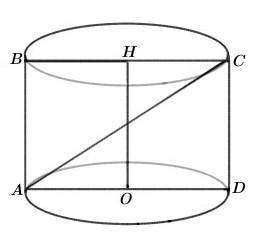
Дано :

Цилиндр.

Прямоугольник ABCD — осевое сечение цилиндра.

ОН — высота цилиндра.

OD = 6 см, OH = 5 см.

Найти :

АС = ?

Образующая и высота цилиндра равны.

Поэтому ОН = CD 5 см.

AD — это диаметр основания цилиндра, поэтому он будет в 2 раза больше радиуса OD. То есть AD = 2×OD = 2×6 см = 12 см.

Рассмотрим ∆ACD — прямоугольный (∠D = 90°).

По теореме Пифагора : AC² = AD² + CD² = 12² + 5² = 144 + 25 = 169⇒AC = √169 = 13 см.

13 см.


НУЖНА Радиус основания цилиндра равен 6 см а высота 5 см. Найдите диагональ осевого сечения цилиндра

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS