tushenka88

26.07.2022 03:23

Геометрия

Есть ответ 👍

Периметр квадрата 60 см.найдите периметр прямоугольника равновеликого квадрату,если стороны прямоугольника относятся как 4: 1

257

380

Посмотреть ответы 2

Ответы на вопрос:

Лизза111

Геометрия

4,5(11 оценок)

р кв.=4у

у=60: 4=15 (см) - сторона квадрата

s кв.=у*у

s кв.=15*15=225 (кв.см)

по условию s кв.=s прямоуг.

s прямоуг.=a*b

a/b=4/1 => a=4b

s прямоуг.=a*b=4b*b=4b^2

b^2=s прямоуг./4

b=√s прямоуг./4

b=√225/4=15/2=7,5 (см) - ширина прямоугольника

а=4*7,5=30 (см) - длина прямоугольника

р=2(a+b)

p прямоуг.=2*(7,5+30)=2*37,5=75 (см)

ответ: периметр прямоугольника 75 сантиметров.

yanix2020

Геометрия

4,4(34 оценок)

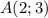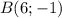Ці точки лежать на серединному перпендикулярі точок A(2;3) та B(6;-1) . Знайдемо координати точки — середини відрізка :

$M\left(\dfrac{2+6}{2};\dfrac{3+(-1)}{2}\right)=M(4;1)$

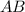Щоб знайти кутовий коефицієнт серединного перпендикуляра, знайдемо кутовий коефіцієнт прямої :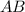

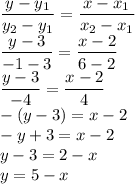
$\dfrac{y-y_1}{y_2-y_1}=\dfrac{x-x_1}{x_2-x_1}\\\dfrac{y-3}{-1-3}=\dfrac{x-2}{6-2}\\\dfrac{y-3}{-4}=\dfrac{x-2}{4}\\-(y-3)=x-2\\-y+3=x-2\\y-3=2-x\\y=5-x$

Коефіцієнт перпендикулярної прямої дорівнює $-\dfrac{1}{-1}=1$ . Застосуємо формулу прямої за кутовим коефицієнтом і точкою, через яку пряма проходить:

$y=kx+b\\1=4+b\\b=-3$

Тобто серединний перпендикуляр має формулу y=x-3 .

Знайдемо точку його перетину:

а) З віссю абсцисс:

$\begin{cases}y=0 \\ y=x-3\end{cases}\\x=3$

Тобто точка має координати (3; 0).

б) З віссю ординат:

$\begin{cases}x=0\\ y=x-3\end{cases}\\y=-3$

Все зобразив на графіку. Перемалюйте його в зошит, щоб отримати вищу оцінку ;)

Відповідь:

а) (3; 0)

б) (0; –3)

Знайдіть точку, яка рівновіддалена від точок (2; 3) і (6; -1) та лежить: а) на осі абсцис; б) на осі

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.