Найдите значение выражения 7х0 + 3у0, если координаты точки а(х0 ; у0) являются решинием системы уравнений
209
449
Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Вопрос отает 1)значения выражения 2-3х меньше 4. 2)значения выражения 2-3х больше...
 avazjon229610.11.2020 11:15
avazjon229610.11.2020 11:15 -
Сделать номер 4. только ответы....
 kamallm712oxbgkk09.12.2021 07:01
kamallm712oxbgkk09.12.2021 07:01 -
Найдите сумму членов геметрической прогрессии со второго по пятый 1/2 , -1/...
 Deyzer77706.01.2020 23:08
Deyzer77706.01.2020 23:08 -
Упростить выражения! за правильные ответы!...
 police528.10.2022 04:12
police528.10.2022 04:12 -
решить Карточка по алгебре 7класс....
 yaritos03.03.2021 06:42
yaritos03.03.2021 06:42 -
постройте систему координат (возьмите единичные отрезки на осях, равные 2 клеткам....
 Taekook1904.03.2020 02:43
Taekook1904.03.2020 02:43 -
Первый вопрос :Какова сумма всех целых решений неравенства - 92 Второй вопрос...
 MegaCrisp109.03.2021 12:36
MegaCrisp109.03.2021 12:36 -
Найдите корень уравнения 5х+5-8х=9+2х-4...
 vikysikrusinova31.07.2020 22:39
vikysikrusinova31.07.2020 22:39 -
4( -7 - х) - 5х = 8 как?...
 Даниил55577720.01.2023 21:20
Даниил55577720.01.2023 21:20 -
с алгеброй полный ответ...
 Whitecat11104.01.2022 17:09
Whitecat11104.01.2022 17:09

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

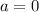
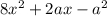 на множители, для чего найдем корни квадратного трехчлена, используя формулу дискриминанта:
на множители, для чего найдем корни квадратного трехчлена, используя формулу дискриминанта: 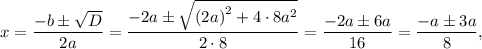
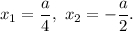
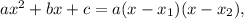 то
то 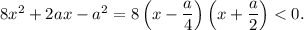
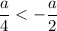 или
или 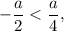 такое неравенство будет иметь решение в виде интервала.
такое неравенство будет иметь решение в виде интервала.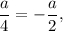 т. е.
т. е. 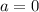 неравенство не будет иметь решений.
неравенство не будет иметь решений.