Алгебра: Формула тождества как решить -3(x-1)+2(2-x)=

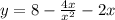
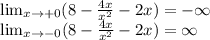
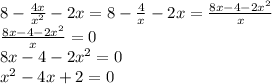
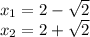
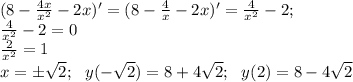
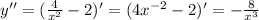
Объяснение:На 0 делить нельзя. Область определения: (-∞;0)∪(0;∞)Т.к х не равен 0, то точек пересечения с осью у нет. Находим точки пересечения с осью х.Решаем квадратное уравнение, находим точки пересечения с осью х:Находим точки экстремума (производная равна нулю).Для нахождения точек перегиба находим вторую производнуюВторая производная нигде не равна нулю, точек перегиба нет.Горизонтальных асимптот нет. 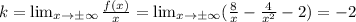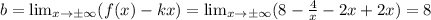Вертикальная асимптота одна: х=0.Ищем наклонную асимптоту:Наклонная асимптота есть:Дальнейшее...

СулеймановаНигяр

14.01.2021 06:13

Алгебра

Есть ответ 👍

Формула тождества как решить
-3(x-1)+2(2-x)=

200

248

Посмотреть ответы 3

Ответы на вопрос:

втклр

Алгебра

4,4(71 оценок)

ответ:

7-5х

объяснение:

-3х+3+4-2х=7-5х

ели равно нулю, то 1,4

maksym200178

Алгебра

4,4(29 оценок)

ответ:

-3(x-1)+2(2-x)=-3x+3+4-2x=7-5x

объяснение:

оарташ

Алгебра

4,7(4 оценок)

Объяснение:

$y=8-\frac{4x}{x^2}-2x$

На 0 делить нельзя. Область определения: (-∞;0)∪(0;∞)

$\lim_{x \to +0} (8-\frac{4x}{x^2}-2x)=-\infty \\ \lim_{x \to -0} (8-\frac{4x}{x^2}-2x)=\infty$

Т.к х не равен 0, то точек пересечения с осью у нет. Находим точки пересечения с осью х.

$8-\frac{4x}{x^2}-2x=8-\frac{4}{x}-2x=\frac{8x-4-2x^2}{x}\\ \frac{8x-4-2x^2}{x}=0\\8x-4-2x^2=0\\x^2-4x+2=0$

Решаем квадратное уравнение, находим точки пересечения с осью х:

$x_1=2-\sqrt{2} \\x_2=2+\sqrt{2}$

Находим точки экстремума (производная равна нулю).

$(8-\frac{4x}{x^2}-2x)'=(8-\frac{4}{x}-2x)'=\frac{4}{x^2}-2;\\ \frac{4}{x^2}-2=0\\ \frac{2}{x^2}=1\\x=\pm \sqrt{2};\ \ y(-\sqrt{2})=8+4\sqrt{2};\ \ y(2)=8-4\sqrt{2}$

Для нахождения точек перегиба находим вторую производную

$y''=(\frac{4}{x^2}-2)'= (4x^{-2}-2)'=-\frac{8}{x^3}$

Вторая производная нигде не равна нулю, точек перегиба нет.

Горизонтальных асимптот нет. Вертикальная асимптота одна: х=0.

Ищем наклонную асимптоту:

$k= \lim_{x \to \pm \infty} \frac{f(x)}{x}= \lim_{x \to \pm \infty} (\frac{8}{x}-\frac{4}{x^2}-2 )=-2$

$b= \lim_{x \to \pm \infty} (f(x)}-k{x})= \lim_{x \to \pm \infty} (8-\frac{4}{x}-2x+2x )=8$

Наклонная асимптота есть:

y=-2x+8

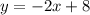
Дальнейшее исследование проводим, заполняя таблицу (см. рис.1).

Постройте график функции: y=8-4x/x^2-2x.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.