Регистрация Спросить otvet5GPT
Брат220
08.02.2022 07:43
Математика
Есть ответ 👍

Существуют ли целые числа x, y, z для которых

(3x - y)(3y - z)(3z - x) = 2001?

128
293
Посмотреть ответы 3

Ответы на вопрос:

ляпрпммм
ляпрпммм
4,8(96 оценок)

ответ:

пошаговое объяснение:

апапапапапапапдщ

elenazeleneckaya
elenazeleneckaya
4,8(5 оценок)

ответ: 3x - 5y - 9z = 0

3x - 9z = 5y

3(x - 3z) = 5y

(x - 3z)/5 = y/3

это значит, что y делится на 3, x - 3z делится на 5, и результаты равны

нам известно, что

55 < = x + y + z < = 59

и все числа целые. значит, возможны варианты:

x + y + z = 55; 56; 57; 58 или 59.

обозначим

(x - 3z)/5 = y/3 = k

тогда

x - 3z = 5k; y = 3k; x = 3z + 5k

x + y + z = 3z + 5k + 3k + z = 4z + 8k = 4(z + 2k) - делится на 4.

из всех возможных сумм только 56 делится на 4.

это и есть сумма. возможны такие решения:

x + y + z = 56

y = 0; (x - 3z)/5 = 0; x = 3z; 4z = 56; z = 14; x = 42

y = 12; (x - 3z)/5 = 4; x = 3z + 20; 4z + 20 + 12 = 56; z = 6; x = 38

y = 24; (x - 3z)/5 = 8; x = 3z + 40; 4z + 40 + 24 = 56; z = -2; x = 34

ответ: 56

неограниченные возможности для обучения без рекламы со знаниями плюс

попробуй сегодня

подробнее - на -

пошаговое объяснение:

sobkevichbozhep08t40
sobkevichbozhep08t40
4,7(41 оценок)

4/3

Пошаговое объяснение:

Площадь будет равно двойному интеграли, взятому по привой области между линиями

Точки пересечения  - решение системы уравнений

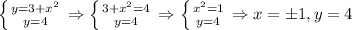
\left \{ {{y=3+x^2} \atop {y=4}} \right\Rightarrow \left \{ {{3+x^2=4} \atop {y=4}} \right\Rightarrow \left \{ {{x^2=1} \atop {y=4}} \right\Rightarrow x=\pm1, y=4

На интервале (-1,1)  линия  y=4 лежит выше кривой 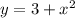y=3+x^2,

поэтому 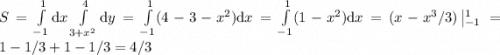S=\int\limits_{-1}^{1}{\rm d}x\int\limits_{3+x^2}^{4}{\rm d}y=\int\limits_{-1}^{1}(4-3-x^2){\rm d} x=\int\limits_{-1}^1(1-x^2) {\rm d} x=(x-x^3/3)\left|_{-1}^1 \right=1-1/3+1-1/3=4/3

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS