Регистрация Спросить otvet5GPT
karinemirova2
19.09.2022 13:51
Математика
Есть ответ 👍

Совершил 3 ошибки в 12 примерах. какую оценку за это нужно поставить

186
389
Посмотреть ответы 2

Ответы на вопрос:

n2324
n2324
4,4(32 оценок)

ответ:

ну тут мне кажется зависят сами примеры.

а так как я знаю 0-1 ошибка 5; 2-3 ошибки 4; 4-7 ошибок 3; 8-10 ошибок 2; 11-12 ошибок 1;

ксения23242526
ксения23242526
4,4(17 оценок)

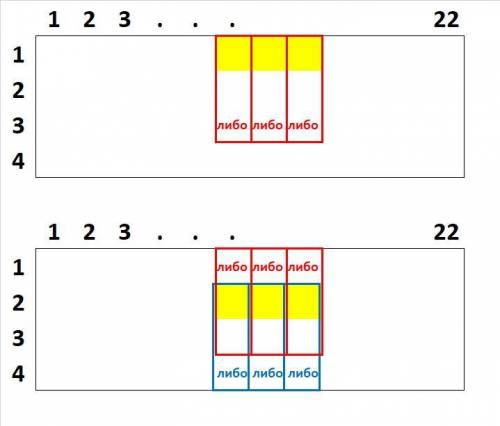
Пусть, горизонтальный прямоугольник уже размещен. Тогда, искомая вероятность - вероятность того, что вертикальный прямоугольник будет пересекать горизонтальный. Заметим, что пересечение возможно только в одной клетке.

Рассмотрим две ситуации.

1. Горизонтальный прямоугольник лежит в крайней (верхней или нижней) строке. Так как всего строк 4, то это может произойти с вероятностью 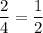\dfrac{2}{4} =\dfrac{1}{2}. Найдем общее число возможных расположений вертикального прямоугольника и число расположений, при которых он пересекается с горизонтальным.

Так как высота вертикального прямоугольника 3, а высота исходного прямоугольника 4, то в каждом столбце вертикальный прямоугольник моет располагаться двумя Таким образом, общее число расположений вертикального прямоугольника равно 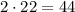2\cdot22=44.

Вертикальный прямоугольник будет пересекаться с горизонтальным в 3 случаях: если он будет располагаться в одном из столбцов, через которые проходит горизонтальный прямоугольник и примыкать к соответствующей крайней строке. Значит, число расположений вертикального прямоугольника, при которых он пересекается с горизонтальным, равно 3.

Учитывая вероятность появления этой ситуации, получим, что пересечение в этой ситуации происходит с вероятностью 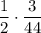\dfrac{1}{2} \cdot\dfrac{3}{44}.

2. Горизонтальный прямоугольник не лежит в крайней строке. Таких строк тоже 2, значит произойти это может также с вероятностью 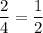\dfrac{2}{4} =\dfrac{1}{2}.

Общее число расположений вертикального прямоугольника по-прежнему равно 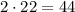2\cdot22=44.

Вертикальный прямоугольник будет пересекаться с горизонтальным, если он будет располагаться в одном из столбцов, через которые проходит горизонтальный прямоугольник, причем располагаться в конкретном столбце он может любым из двух возможных Значит, число расположений вертикального прямоугольника, при которых он пересекается с горизонтальным, равно 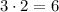3\cdot2=6.

Учитывая вероятность появления этой ситуации, получим, что пересечение в этой ситуации происходит с вероятностью 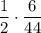\dfrac{1}{2} \cdot\dfrac{6}{44}.

Рассмотренные ситуации не совместны, так как горизонтальный прямоугольник не может располагаться в двух строках одновременно. Значит, соответствующие вероятности необходимо складывать:

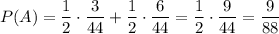
P(A)=\dfrac{1}{2} \cdot\dfrac{3}{44} +\dfrac{1}{2} \cdot\dfrac{6}{44}=\dfrac{1}{2} \cdot\dfrac{9}{44}=\dfrac{9}{88}

ответ: 9/88


Дан клетчатый прямоугольник высоты 4 и ширины 22. Вася красит какой-тогоризонтальный прямоугольник 1

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS