Регистрация Спросить otvet5GPT
ВоительЧерноснежка
22.05.2022 04:08
Алгебра
Есть ответ 👍

С. 19 . 9 класс. тема: уравнение окружности. : составьте уравнение окружности с центром в точке q и радиусом r, если:
1) q (2, -3), r=10
2) q(0; 3), r=2​

141
311
Посмотреть ответы 1

Ответы на вопрос:

Ok7a
Ok7a
4,5(1 оценок)

В решении.

Объяснение:

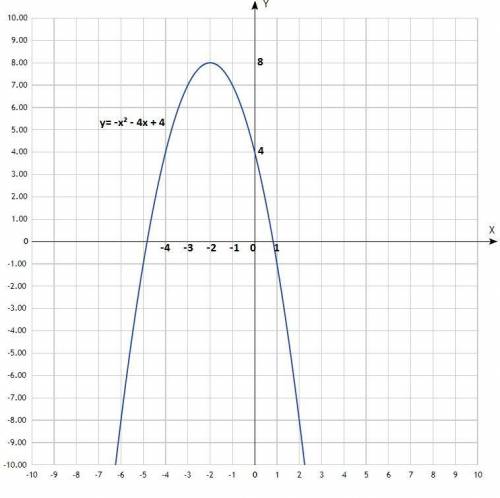
Дана функция у= -х² - 4х + 4;

a) координаты вершин параболы;

1) Найти х₀:

Формула: х₀ = -b/2a;

у= -х² - 4х + 4;

х₀ = 4/-2

х₀ = -2;

2) Найти у₀:

у= -х² - 4х + 4;

у₀ = -(2²) - 4*(-2) + 4 = -4 + 8 + 4 = 8

у₀ = 8;

b) ось симметрии параболы;

Ось симметрии Х = х₀

Х = -2;

c) точки пересечения параболы с осью Ох;

Точки пересечения параболы с осью Ох называются нулями функции (у в этих точках равен нулю).

Приравнять уравнение функции к нулю и решить квадратное уравнение:

-х² - 4х + 4 = 0/-1

х² + 4х - 4 = 0

D=b²-4ac = 16 + 16 = 32        √D=√16*2 = 4√2

х₁=(-b-√D)/2a

х₁=(-4-4√2)/2

х₁= -2 - 2√2 ≈ -4,8;                

х₂=(-b+√D)/2a

х₂=(-4+4√2)/2

х₂= -2 + 2√2 ≈ 0,8;

х₁= -2 - 2√2;  х₂= -2 + 2√2 - нули функции.

d) точки пересечения параболы с осью Оу;

Любой график пересекает ось Оу при х = 0:

у= -х² - 4х + 4;

у = -0² - 4*0 + 4

у = 4;

Парабола пересекает ось Оу при у = 4;

e) постройте график функции;

Уравнение квадратичной функции, график - парабола, ветви направлены вниз, пересекают ось Ох в точках х₁= -2 - 2√2 ≈ -4,8 и

х₂= -2 + 2√2 ≈ 0,8.

Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.

у= -х² - 4х + 4;

    Таблица:

х  -6     -5     -4     -3     -2     -1     0     1     2

у  -8      -1      4      7       8      7     4    -1    -8

По вычисленным точкам построить параболу.


Дана функция у=-х^2-4х+4 a)коррдинаты вершин параболы B)ось симетрии параболы C)точки пересечения

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS