карина2029

15.11.2020 23:33

Геометрия

Есть ответ 👍

Основания трапеции равны 25 и 15, одна из боковых сторон равна 14, а косинус угла между ней и одним из оснований равен 4√3÷7. найдите площадь трапеции

115

374

Посмотреть ответы 1

Ответы на вопрос:

Ухв

Геометрия

4,5(98 оценок)

***

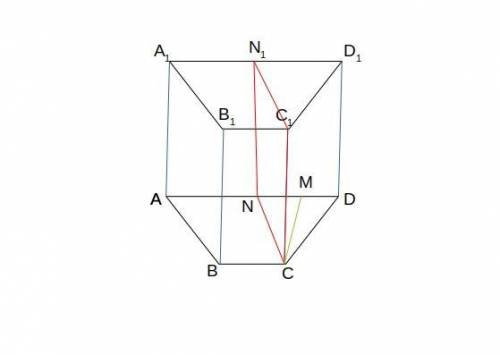
CNN1C1 - прямоугольник

сначала найдем площадь осн.

и поскольку основание призмы у нас трапеция

значит находим площадь трапеции ABCD

площадь трапеции равна произведению полусуммы ее оснований на высоту:

S = ((AD + BC) / 2) · СМ

(где высота трапеции — это перпендикуляр, проведенный из любой точки одного из оснований к прямой,

содержащей другое основание)

пусть ВС - х

АD - 6х

СN - 6х

S (осн.) = (BC + AD) · CM = (6х + х )/ 2 · 6х = 7х / 2 ·6х = 7х · 3х = 21х²

СС₁ = V / S (осн.) = 672 / 21х²

8 = 672 / 21x²

x² = 672 / ( 8 · 21)

x² = 672 / 168

x² = 4

x = √4 = 2 см

ВС = х = 2

АD = 6х = 6 · 2 = 12 = CN

CN║AB

CN = AB

из треугольника СND

треугольник - равнобедренный

CN = CD

CM и медиана , и высота, и биссектриса

(свойства равнобедренного треугольника)

NM = ND = (AD - BC) / 2 = (12-2) /2 = 10/2 = 5 см

∠М = 90°

по теореме Пифагора

сумма квадратов длин катетов равна квадрату длины гипотенузы

т.е.

c² = a² + b²

NC² = NM² + MC²

NC² = (5)² + 12)²

NC = √((5)² + 12)²)

NC = √(25 + 144)

NC= √169

NC = 13 см

поскольку CNN1C1 - прямоугольник

а для того чтобы найти площадь прямоугольника, надо его длину умножить на ширину

S(CNN1C1) = 8 · 13 = 104 см²

ответ: 104 см²

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.