Регистрация Спросить otvet5GPT
V5Ch
15.12.2021 10:16
Алгебра
Есть ответ 👍

Для натуральних чисел m,n,k виконується нерівність m: n> m+k: n+k доведіть що m> n

298
498
Посмотреть ответы 2

Ответы на вопрос:

Voproshayka
Voproshayka
4,8(30 оценок)

\displaystyle \dfrac{m}{n}> \dfrac{m+k}{n+k}~~~\rightarrow~~~\dfrac{m}{n}> \dfrac{m-n+n+k}{n+k}~~~\rightarrow~~\dfrac{m}{n}> \dfrac{m-n}{n+k}+1\\ \\ \\ \dfrac{m}{n}-1> \dfrac{m-n}{n+k}~\rightarrow~ \dfrac{m-n}{n}-\dfrac{m-n}{n+k}> 0~\rightarrow~ (m-n)\left(\dfrac{1}{n}-\dfrac{1}{n+k}\right)> 0\\ \\ \\ (m-n)\cdot \dfrac{n+k-n}{n(n+k)}> 0~~~\rightarrow~~~\dfrac{k}{n(n+k)}\cdot(m-n)> 0

\dfrac{k}{n(n+k)} - натуральное число, разделим последнее неравенство на число \dfrac{k}{n(n+k)}, получим m-n> 0 откуда m> n

доказано.

shopiakprod
shopiakprod
4,4(2 оценок)

1

Объяснение:

Область определения квадратных корней:

x >= 1

Возводим в квадрат

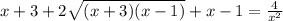
x+3+2\sqrt{(x+3)(x-1)} +x-1=\frac{4}{x^2}

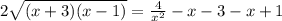
2\sqrt{(x+3)(x-1)} =\frac{4}{x^2} -x-3-x+1

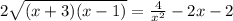
2\sqrt{(x+3)(x-1)} =\frac{4}{x^2} -2x-2

Делим все на 2

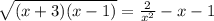
\sqrt{(x+3)(x-1)} =\frac{2}{x^2} -x-1

Умножаем на x^2

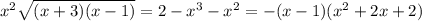
x^2\sqrt{(x+3)(x-1)} =2-x^3-x^2=-(x-1)(x^2+2x+2)

Слева квадрат умножается на арифметический корень, то есть число неотрицательное при любом x >= 1.

Справа первая скобка неотрицательна при x >= 1, вторая скобка положительна при любом х. И стоит минус.

В итоге число получается неположительное.

Единственное значение, при котором левая и правая части обе одновременно равны 0 - это x = 1.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS