Регистрация Спросить otvet5GPT
Cказочник
20.10.2022 19:10
Алгебра
Есть ответ 👍

6х^2-5х+1=0 решите неравенство

120
485
Посмотреть ответы 1

Ответы на вопрос:

vulpe
vulpe
4,4(59 оценок)

1) (3;∞);   2) (0;10]

Объяснение:

1)

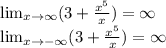
\lim_{x \to \infty} (3+\frac{x^5}{x})=\infty\\ \lim_{x \to -\infty} (3+\frac{x^5}{x})=\infty

Свое экстремальное значение функция примет в точках, где производная равна 0.

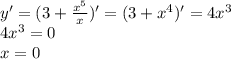
y'=(3+\frac{x^5}{x})'= (3+x^4)'=4x^3\\4x^3=0\\x=0

Найденная точка является точкой разрыва. Найдем пределы справа и слева:

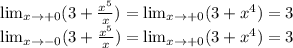
\lim_{x \to +0} (3+\frac{x^5}{x})= \lim_{x \to +0} (3+x^4)= 3\\ \lim_{x \to -0} (3+\frac{x^5}{x})= \lim_{x \to +0} (3+x^4)= 3

Таким образом значения функции меняются от 3 до бесконечности

(3;∞)

2) Находим пределы, используя правило Лопиталя:

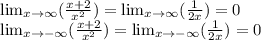
\lim_{x \to \infty} (\frac{x+2}{x^2})=\lim_{x \to \infty} (\frac{1}{2x})=0\\ \lim_{x \to -\infty}(\frac{x+2}{x^2})=\lim_{x \to -\infty} (\frac{1}{2x})=0

Свое экстремальное значение функция примет в точках, где производная равна 0.

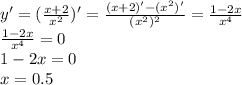
y'=(\frac{x+2}{x^2})'=\frac{(x+2)'-(x^2)'}{(x^2)^2}= \frac{1-2x}{x^4} \\\frac{1-2x}{x^4}=0\\1-2x=0\\x=0.5

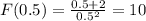
F(0.5)=\frac{0.5+2}{0.5^2}=10

Таким образом значения функции меняются от 0 (не входит) до 10 (входит):

(0;10]

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS