Математика: Найти вторую производную функции y=x^3-2x

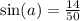
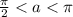
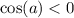
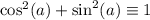
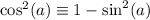
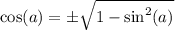
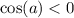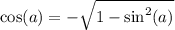
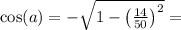
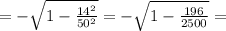
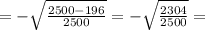
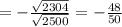
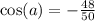
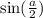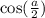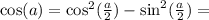
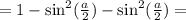
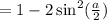
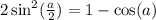
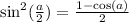
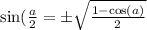
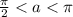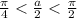
a принадлежит второй четверти, в которой косинус отрицателен,тогда но т.к. , тоитак теперь найдем и . ⇔ а это значит 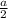принадлежит первой четверти в которой и синус и косинус положительны, поэтому...

вгььсь

14.02.2023 22:21

Математика

Есть ответ 👍

Найти вторую производную функции y=x^3-2x

247

349

Посмотреть ответы 4

Ответы на вопрос:

lexalarionov11

Математика

4,7(89 оценок)

ответ:

решение представлено на фото

sofaTV

Математика

4,7(63 оценок)

Ямогу предположить?

89518099647

Математика

4,4(85 оценок)

Голубым скорее всего

malekovemir

Математика

4,4(32 оценок)

$\sin(a) = \frac{14}{50}$

$\frac{\pi}{2} < a < \pi$

a принадлежит второй четверти, в которой косинус отрицателен,

тогда $\cos(a) < 0$

$\cos^2(a) + \sin^2(a) \equiv 1$

$\cos^2(a) \equiv 1 - \sin^2(a)$

$\cos(a) = \pm\sqrt{1 - \sin^2(a)}$

но т.к. $\cos(a) < 0$ , то

$\cos(a) = -\sqrt{1-\sin^2(a)}$

$\cos(a) = -\sqrt{1 - \left( \frac{14}{50}\right)^2} =$

$= -\sqrt{1 - \frac{14^2}{50^2}} = -\sqrt{1 - \frac{196}{2500}} =$

$= -\sqrt{\frac{2500 - 196}{2500}} = -\sqrt{\frac{2304}{2500}} =$

$= -\frac{\sqrt{2304}}{\sqrt{2500}} = -\frac{48}{50}$

итак $\cos(a) = -\frac{48}{50}$

теперь найдем $\sin(\frac{a}{2})$ и $\cos(\frac{a}{2})$ .

$\cos(a) = \cos^2(\frac{a}{2}) - \sin^2(\frac{a}{2}) =$

$= 1 - \sin^2(\frac{a}{2}) - \sin^2(\frac{a}{2}) =$

$= 1 - 2\sin^2(\frac{a}{2})$

$2\sin^2(\frac{a}{2}) = 1 - \cos(a)$

$\sin^2(\frac{a}{2}) = \frac{1 - \cos(a)}{2}$

$\sin(\frac{a}{2} = \pm\sqrt{\frac{1-\cos(a)}{2}}$

$\frac{\pi}{2} < a < \pi$ ⇔ $\frac{\pi}{4} < \frac{a}{2} < \frac{\pi}{2}$

а это значит $\frac{a}{2}$ принадлежит первой четверти в которой и синус и косинус положительны, поэтому

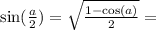
$\sin(\frac{a}{2}) = \sqrt{\frac{1 - \cos(a)}{2}} =$

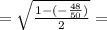
$= \sqrt{\frac{1 - (-\frac{48}{50})}{2}} =$

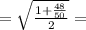
$= \sqrt{\frac{1 + \frac{48}{50}}{2}} =$

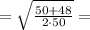
$= \sqrt{\frac{50 + 48}{2\cdot 50}} =$

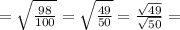
$= \sqrt{\frac{98}{100}} = \sqrt{\frac{49}{50}} = \frac{\sqrt{49}}{\sqrt{50}} =$

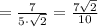
$= \frac{7}{5\cdot\sqrt{2}} = \frac{7\sqrt{2}}{10}$

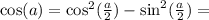
$\cos(a) = \cos^2(\frac{a}{2}) - \sin^2(\frac{a}{2}) =$

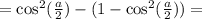
$= \cos^2(\frac{a}{2}) - (1 - \cos^2(\frac{a}{2})) =$

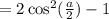
$= 2\cos^2(\frac{a}{2}) - 1$

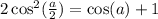
$2\cos^2(\frac{a}{2}) = \cos(a) + 1$

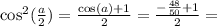
$\cos^2(\frac{a}{2}) = \frac{\cos(a) + 1}{2} = \frac{-\frac{48}{50} + 1}{2} =$

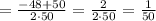
$= \frac{-48 + 50}{2\cdot 50} = \frac{2}{2\cdot 50} = \frac{1}{50}$

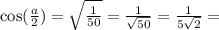
$\cos(\frac{a}{2}) = \sqrt{\frac{1}{50}} = \frac{1}{\sqrt{50}} = \frac{1}{5\sqrt{2}} =$

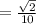
$= \frac{\sqrt{2}}{10}$

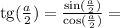
$\mathrm{tg}(\frac{a}{2}) = \frac{\sin(\frac{a}{2})}{\cos(\frac{a}{2})} =$

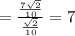
$= \frac{\frac{7\sqrt{2}}{10}}{\frac{\sqrt{2}}{10}} = 7$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.