Найти sin a,если cos a= корень из 15 делённая на 8 и принадлежит (число пи; 3 пи на 2) ,!
166
232
Ответы на вопрос:
ответ: sina=-7/8.
пошаговое объяснение:
cosa=-√15/8 π
sin²a+cos²a=1
sin²a=1-cos²a=1-(-√15/8)²=1-(15/64)=49/64
sina=√(49/64)=±7/8
так как a∈(π; 3π/2) ⇒
sina=-7/8.
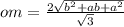
Пошаговое объяснение:
рассмотрим треугольники ОВК и АВК. Они прямоугольные и у них общий острый угол К=30°, следовательно они подобны по первому признаку:
∆ОВК ~ ∆АМК. Найдём по теореме Пифагора катет АК в ∆АМК: АК²=МК²–АМ²=(2а)²–а²=4а²–а²=3а²; АК=√(3а²)=а√3
ВК=ВМ+МК=b+2a
Так как ∆АМК ~ ∆ОВК, то:
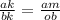
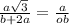
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
а√3×ОВ=а(b+2a)
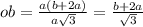
Рассмотрим ∆ОВМ. В нём известны два катета ОВ и ВМ и теперь найдём ОМ по теореме Пифагора:
ОМ²=ОВ²+ВМ²=
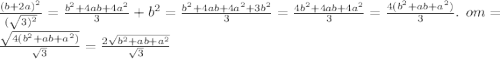
PS: om - это ОМ маленькими английскими буквами
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Выразите в часах 29 минут;30 минут ;48 минут...
 andrejisaev20Andrey17.06.2022 07:41
andrejisaev20Andrey17.06.2022 07:41 -
Какие из перечисленных чисел меньше чем 17 /33 Отметьте все соответствующие...
 erro1410.06.2023 23:15
erro1410.06.2023 23:15 -
найдите угловой коэффициент касательной, проведённой к графику функции y=...
 nastaklimenkofll12.08.2020 17:58
nastaklimenkofll12.08.2020 17:58 -
У першому парку було 48 баків для скляного посуду, а в другому 44. З першого...
 Foxyinfog21.07.2022 02:14
Foxyinfog21.07.2022 02:14 -
1. Изобразите на координатной прямой и запишите пересечение и объединение...
 elichev322.06.2022 22:14
elichev322.06.2022 22:14 -
№2 Дана функция : 3х2 – 2x – 1. а) Найдите значения функции f (-2); f(6) [2]...
 AlenaRayskaya25.01.2020 21:17
AlenaRayskaya25.01.2020 21:17 -
Знайдите два лики,адин з яких у 4разоу больштза други,кали их сума роуна 15...
 Arestan03.11.2021 16:22
Arestan03.11.2021 16:22 -
очень : Определите объем аквариума, если его длина 1м, ширина в 2 раза меньше...
 guast131.01.2022 13:39
guast131.01.2022 13:39 -
. Мне надо сделать с решением...
 Ушастый120930.01.2022 08:27
Ушастый120930.01.2022 08:27 -
CРОЧНО!! Провести касательную к прямой,...
 MariaUt15.12.2021 20:58
MariaUt15.12.2021 20:58

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
