1вычислите поверхности и объем пирамиды, если в её основании лежит равносторонний треугольник со стороной 6 м, боковое ребро равно 5 м, а высота пирамиды корень из 32 стороны основания прямой четырехугольной призмы равны 8 см и 15 см и образуют угол 60 градусов найдите площадь полной поверхности и объема призмы если высота 10 см

261

440

Посмотреть ответы 1

Ответы на вопрос:

baburina56vValiabab

Геометрия

4,5(65 оценок)

$sin^{4} a-cos^{4} a+1=2sin^{2} a\\(sin^{2} a-cos^{2} a)(sin^{2} a+cos^{2} a)+1=2sin^{2} a\\(sin^{2} a-cos^{2} a)*1+1=2sin^{2} a\\sin^{2} a-cos^{2} a+1=2sin^{2} a\\sin^{2} a+(1-cos^{2} a)=2sin^{2} a\\sin^{2} a+sin^{2} a=2sin^{2} a$

Объяснение:

Нужно доказать, что правая и левая части тождества равны.

Рассмотрим левую часть тождества: 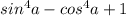$sin^{4} a-cos^{4} a+1$

Вспомним

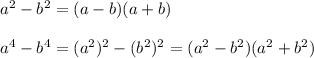
$a^{2} -b^{2} =(a-b)(a+b)a^{4} -b^{4} =(a^{2})^{2} -(b^{2})^{2} =(a^{2} -b^{2})(a^{2} +b^{2})\\$

Тогда:

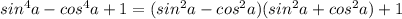
$sin^{4} a-cos^{4} a+1=(sin^{2} a-cos^{2} a)(sin^{2} a+cos^{2} a)+1\\$

Вспомним:

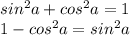
$sin^{2} a+cos^{2} a=1\\1-cos^{2} a=sin^{2} a$

Тогда:

$(sin^{2} a-cos^{2} a)(sin^{2} a+cos^{2} a)+1=(sin^{2} a-cos^{2} a)*1+1=sin^{2} a-cos^{2} a+1==sin^{2} a+(1-cos^{2} a)=sin^{2} a+sin^{2} a=2sin^{2} a$

То есть правая часть тождества равна левой. Тождество доказано.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.