Найди значение выражения k: 8, если k приоб-ретает значения: 16, 24, 40, 64.

142

424

Посмотреть ответы 1

Ответы на вопрос:

prohorowanyura

Математика

4,6(69 оценок)

Пошаговое объяснение:

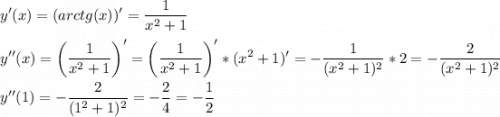
$\displaystyle y'(x)=(arctg(x))'=\frac{1}{x^2+1} y''(x)=\bigg (\frac{1}{x^2+1 } \bigg )'=\bigg (\frac{1}{x^2+1 } \bigg )'*(x^2+1)'=-\frac{1}{(x^2+1)^2} *2=-\frac{2}{(x^2+1)^2} y''(1)=-\frac{2}{(1^2+1)^2} =-\frac{2}{4} =-\frac{1}{2}$

$\displaystyle y'(x)=(sin^2(x))' = (sin^2(x))'*(sin(x))'=2sin(x)cos(x)\\y''(x)= \bigg (2sin(x)cos(x)\bigg )'=2(sin(x))'*cosx +2sin(x)*(cos(x))' = qquad =2cos(x)*cos(x)+2sin(x)*(-sin(x) = 2(cos^2(x)-sin^2(x)) = 2cos(2x)y''\bigg (\frac{\pi}{6} \bigg )=2cos \bigg(2*\frac{\pi}{6}\bigg ) =2cos\bigg (\frac{\pi}{3} \bigg )=2*\frac{1}{2} =1$

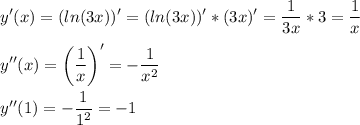
$\displaystyle y'(x)=(ln(3x))' = (ln(3x))'*(3x)'=\frac{1}{3x} *3=\frac{1}{x} y''(x) = \bigg (\frac{1}{x} \bigg )' = -\frac{1}{x^2} y''(1) = -\frac{1}{1^2} =-1$

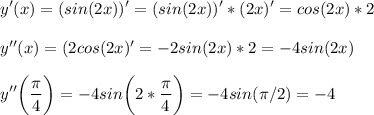
$\displaystyle y'(x) = (sin(2x))' = (sin(2x))' *(2x)'=cos(2x)*2y''(x) = (2cos(2x)' = -2sin(2x)*2=-4sin(2x)y''\bigg (\frac{\pi}{4} \bigg )=-4sin\bigg (2*\frac{\pi}{4} \bigg )=-4sin(\pi/2)=-4$

первая производная неявно заданной функции по формуле

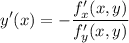
$\displaystyle y'(x) = -\frac{f'_x(x,y)}{f'_y(x,y)}$

помним, что при нахождении 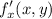$\displaystyle f'_x(x,y)$ y считаем константой, а при нахождении 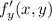$\displaystyle f'_y(x,y)$ константой считаем х

$\displaystyle f'_x(x,y)=(x^2-xy+y^2)'=2x-yf'_y(x,y) = -x+2y$

тогда

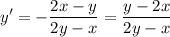
$\displaystyle y'=-\frac{2x-y}{2y-x} =\frac{y-2x}{2y-x}$

ну а дальше надо дифференцировать у'

это попозже чуток...

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.