Регистрация Спросить otvet5GPT
pollvasiltv
18.11.2020 09:45
Математика
Есть ответ 👍

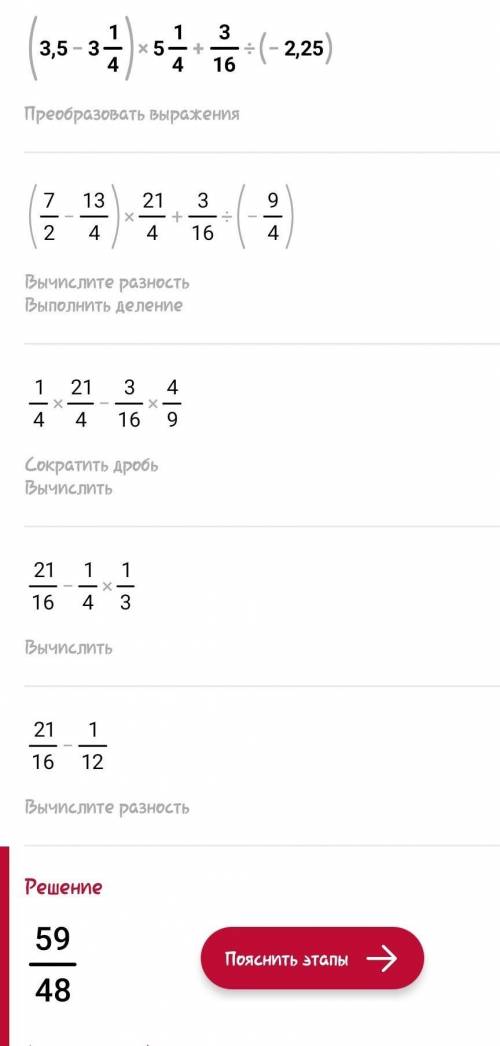
1. даны векторы а1 а2 а3 и вектор в, в некотором базисе трехмерного пространства. показать, что векторы образуют базис данного трехмерного пространства и найти координаты вектора в этом базисе.1.1. (7; 2; 1), (4; 3; 5), (3; 4; -2), (2; -5; -13). ты разбираешься? определитель -129 что дальше делать?

120
491
Посмотреть ответы 2

Ответы на вопрос:

mixfix2017
mixfix2017
4,8(75 оценок)
Базис в пространства состоит из независимых векторов, так, что отсюда следует: чтоб доказать что три вектора базис для нужно показать что векторы независимы. самый простой для этого способ - матрицу состоящую из этих векторов к треугольному виду. по теореме - "ненулевые строки в треугольной матрице - независимы" получим доказательство/опровержение. дальше следует преобразование вектора по базису в. самый простой способ это сделать - решить: где и если возникнут вопросы - пиши.
devochkaSlava
devochkaSlava
4,5(38 оценок)

Пошаговое объяснение:

если я правильно записала пример, то вот ответ


Найдите значения выражения: (3,5 - 3 1/4) × (5 1/4) + 3/16 : (-2,25)

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS