maksimmaksegoroysa5l

27.05.2023 11:50

Математика

Есть ответ 👍

Изобразить на координатных прямых решение неравенств: 1)|х|≤5,6 2)|х|< 17 3)|х|> 4 3/16 4)|х|≥9

228

410

Посмотреть ответы 1

Ответы на вопрос:

defordd

Математика

4,4(27 оценок)

Пошаговое объяснение:

Пусть одна из сторон основания такой призмы - х, и ее высота - h. Тогда периметр ее боковой стороны - 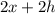2x+2h и он равен 12.

Найдем объём такой призмы.

Объем призмы - площадь основания (в данном случае треугольника) умноженный на высоту (h)

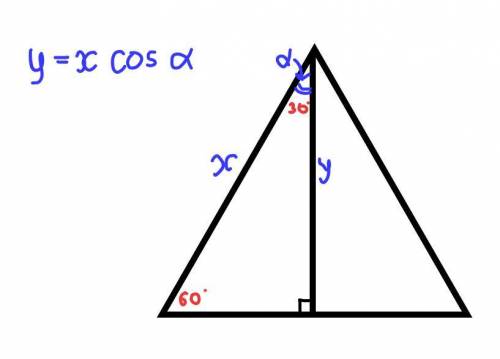
Найдём площадь треугольника в основании (см. рис. 1.)

1) проведём высоту у. Тогда площадь этого треугольника будет равна 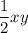$\displaystyle \frac12xy$

После проведения высоты у нас оказался прямоугольный треугольник со сторонами x и y, и углом между ними в 30°

Тогда его площадь -

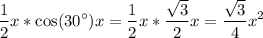
$\displaystyle \frac12x*\cos(30\а)x = \frac12x*\frac{\sqrt3}2x=\frac{\sqrt3}4x^2$

Выразим h через х: 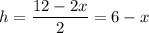$\displaystyle h=\frac{12-2x}2=6-x$

Подставим в формулу объема:

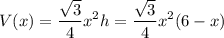
$\displaystyle V(x)=\frac{\sqrt3}4x^2h=\frac{\sqrt3}4x^2(6-x)$

Найдём экстремумы функции:

1) Найдем производную:

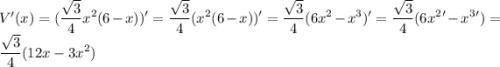
$V'(x)=\displaystyle (\frac{\sqrt3}4x^2(6-x))'=\frac{\sqrt3}4(x^2(6-x))'=\frac{\sqrt3}4(6x^2-x^3)'=\frac{\sqrt3}4(6x^2'-x^3')=\frac{\sqrt3}4(12x-3x^2)$

Приравняем её к 0

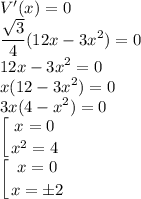
$V'(x)=0\displaystyle \\\frac{\sqrt3}4(12x-3x^2)=0\\12x-3x^2=0\\x(12-3x^2)=0\\3x(4-x^2)=0\\\left [ {{x=0} \atop {x^2=4}} \right. \\\left [ {{x=0} \atop {x=\pm2}} \right.$

Поскольку у нас геометрия и таких страшных штук как отрицательные стороны у нас нет. Осталось только выбрать между 2 и 0.

Если 0, то это вообще не призма, знак производной говорит тоже самое.

Тогда подходит 2.

И это ответ!

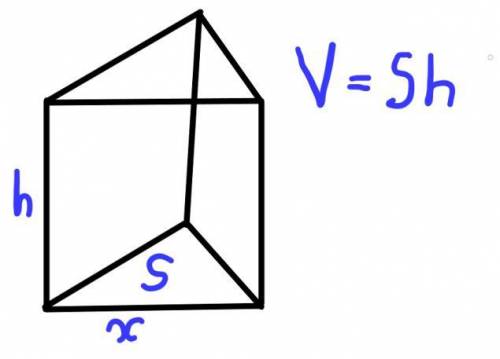
Периметр боковой грани правильной треугольной призмы равен 12 см. При какой длине стороны основания

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.