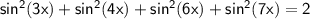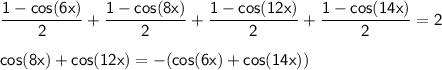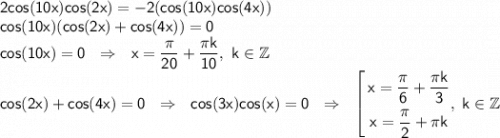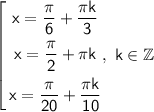Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Pізниця між сьомим і п ятим членами геометричної прогресії дорівнює 96, сума...
 megasashabori07.02.2020 23:37
megasashabori07.02.2020 23:37 -
Шостий член геометричної прогресії складає 60 % від третього члена тієі ж...
 Raz1elGG23.01.2021 15:27
Raz1elGG23.01.2021 15:27 -
Обчисли наступні 3 члена геометричної прогресії, якщо b1 = 2 і знаменник дорівнює...
 андрей214906.09.2022 05:21
андрей214906.09.2022 05:21 -
Вычисли y(2), если y(s)= s−4,8. ...
 диас16114.02.2022 11:58
диас16114.02.2022 11:58 -
Определи y(4), если y(t)= 8,5+t....
 vitiatiger04.09.2022 13:26
vitiatiger04.09.2022 13:26 -
Знайдіть відстань від точки кола до діаметра та до його кінців, якщо висота...
 alidniva11127.01.2020 20:16
alidniva11127.01.2020 20:16 -
Найдите значение выражения...
 Regina39115.01.2022 01:30
Regina39115.01.2022 01:30 -
Известно, что треугольник ABC равен треугольнику DEK. Если AB = 7, то 1) DK...
 Dirijabl24.01.2020 06:36
Dirijabl24.01.2020 06:36 -
На координатной прямой даны точки A(−3) и B(9). M — середина отрезка AB. 7kl.11..png...
 СараАмилина20.04.2022 09:16
СараАмилина20.04.2022 09:16 -
очень надо!! Человек нажимает на лопату силой 600Н. Определи, какое давление...
 крымнаш01.10.2020 03:39
крымнаш01.10.2020 03:39

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.