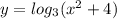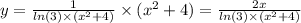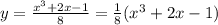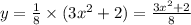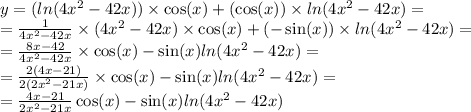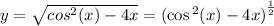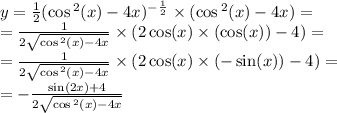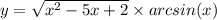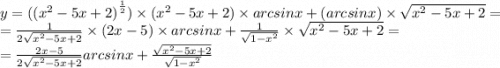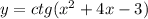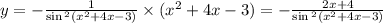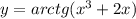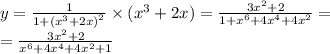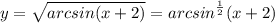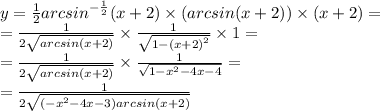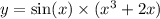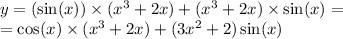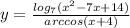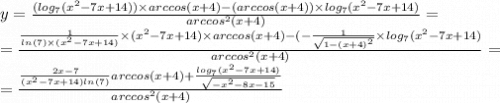Регистрация Спросить otvet5GPT
missislevitina
14.09.2022 23:54
Математика
Есть ответ 👍

Природные явления геологического, метеорологического, гидрологического и биологического происхождения в воронежской области

138
413
Посмотреть ответы 2

Ответы на вопрос:

valu49
valu49
4,7(15 оценок)
Природа, (природная) среда играет важную роль в жизни и развитии человеческого общества. природа в широком смысле слова охватывает весь материальный мир. среда - часть природы, которая непосредственно связана с жизнью и деятельностью общества, взаимодействует с ним.  важнейшая особенность (природной) среды - территориальная неоднородность, делает ее одним из главных факторов расселения людей и размещения производства.
YarMax
YarMax
4,8(12 оценок)

1.

y = log_{3}( {x}^{2} + 4 )

y = \frac{1}{ ln(3) \times ( {x}^{2} + 4)} \times ( {x}^{2} + 4) = \frac{2x}{ ln(3) \times ( {x}^{2} + 4) } \\

2.

y = \frac{ {x}^{3} + 2x - 1}{8} = \frac{1}{8} ( {x}^{3} + 2x - 1) \\

y = \frac{1}{8} \times (3 {x}^{2} + 2) = \frac{3 {x}^{2} + 2 }{8} \\

3.

y = ln(4 {x}^{2} - 42x) \cos(x)

y = ( ln(4 {x}^{2} - 42x)) \times \cos(x) + (\cos(x)) \times ln(4 {x}^{2} - 42x) = \\ = \frac{1}{4 {x}^{2} - 42x} \times (4 {x}^{2} - 42 {x}) \times \cos(x) + ( - \sin(x)) \times ln(4 {x}^{2} - 42x ) = \\ = \frac{8x - 42}{4 {x}^{2} - 42x} \times \cos(x) - \sin(x) ln(4 {x}^{2} - 42x) = \\ = \frac{2(4x - 21)}{2(2 {x}^{2} - 21x) } \times \cos(x) - \sin(x) ln(4 {x}^{2} - 42x) = \\ = \frac{4x - 21}{2 {x}^{2} - 21x} \cos(x) - \sin(x) ln(4 {x}^{2} - 42x)

4.

y = \sqrt{cos {}^{2}(x) - 4x} = {( \cos {}^{2} (x) - 4x)}^{ \frac{1}{2} } \\

y = \frac{1}{2} ( \cos {}^{2} (x) - 4x) {}^{ - { \frac{1}{2} }^{} } \times ( \cos {}^{2} (x) - 4x) = \\ = \frac{1}{2 \sqrt{ \cos {}^{2} (x) - 4x } } \times (2 \cos(x) \times ( \cos(x)) - 4) = \\ = \frac{1}{2 \sqrt{ \cos {}^{2} (x) - 4x } } \times (2 \cos(x) \times ( - \sin(x)) - 4) = \\ = - \frac{ \sin(2x) + 4 }{2 \sqrt{ \cos {}^{2} (x) - 4x } }

5.

y = \sqrt{ {x}^{2} - 5x + 2 } \times arcsin(x)

y = ( {( {x}^{2} - 5x + 2) }^{ \frac{1}{2} } ) \times ( {x}^{2} - 5x + 2) \times arcsinx + (arcsin x) \times \sqrt{ {x}^{2} - 5x + 2} = \\ = \frac{1}{2 \sqrt{ {x}^{2} - 5x + 2} } \times (2x - 5) \times arcsinx + \frac{1}{ \sqrt{1 - {x}^{2} } } \times \sqrt{ {x}^{2} - 5x + 2} = \\ = \frac{2x - 5}{2 \sqrt{ {x}^{2} - 5x + 2} } arcsinx + \frac{ \sqrt{ {x}^{2} - 5x + 2} }{ \sqrt{1 - {x}^{2} } }

6.

y = ctg( {x}^{2} + 4x - 3)

y = - \frac{1}{ \sin {}^{2} ( {x}^{2} + 4x - 3) } \times ( {x}^{2} + 4x - 3) = - \frac{2x + 4}{ \sin {}^{2} ( {x}^{2} + 4x - 3) } \\

7.

y = arctg( {x}^{3} + 2x)

y = \frac{1}{1 + {( {x}^{3} + 2x) }^{2} } \times ( {x}^{3} + 2x) = \frac{3 {x}^{2} + 2}{1 + {x}^{6} + 4 {x}^{4} + 4 {x}^{2} } = \\ = \frac{3 {x}^{2} + 2 }{ {x}^{6} + 4 {x}^{4} + 4 {x}^{2} + 1 }

8.

y = \sqrt{arcsin(x + 2)} = {arcsin}^{ \frac{1}{2} } (x + 2) \\

y = \frac{1}{2} {arcsin}^{ - \frac{1}{2}}(x + 2) \times ( arcsin(x + 2)) \times (x + 2) = \\ = \frac{1}{2 \sqrt{arcsin(x + 2)} } \times \frac{1}{ \sqrt{1 - {(x + 2)}^{2} } } \times 1 = \\ = \frac{1}{2 \sqrt{arcsin(x + 2)} } \times \frac{1}{ \sqrt{1 - {x}^{2} - 4x - 4 } } = \\ = \frac{1}{2 \sqrt{( - {x}^{2} - 4x - 3)arcsin(x + 2)} }

9.

y = \sin(x) \times ( {x}^{3} + 2x)

y = ( \sin(x)) \times ( {x}^{3} + 2x) +( {x}^{3} + 2x) \times \sin(x) = \\ = \cos(x) \times ( {x}^{3} + 2x) + (3 {x}^{2} + 2) \sin(x)

10.

y = \frac{ log_{7}( {x}^{2} - 7x + 14) }{arccos(x + 4)} \\

y = \frac{( log_{7}( {x}^{2} - 7x + 14)) \times arccos(x + 4) - (arccos(x + 4)) \times log_{7}( {x}^{2} - 7x + 14) }{ {arccos}^{2} (x + 4)} = \\ = \frac{ \frac{1}{ ln(7) \times ( {x}^{2} - 7x + 14)} \times ( {x}^{2} - 7x + 14) \times arccos(x + 4) - ( - \frac{1}{ \sqrt{1 - {(x + 4)}^{2} } } \times log_{7}( {x}^{2} - 7x + 14 ) }{ {arccos}^{2}(x + 4) } = \\ = \frac{ \frac{2x - 7}{( {x}^{2} - 7x + 14) ln(7) }arccos (x + 4) + \frac{ log_{7}( {x}^{2} - 7x + 14 ) }{ \sqrt{ - {x}^{2} - 8x - 15} } }{arccos {}^{2} (x + 4)}

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS