MAN1337228

02.07.2020 23:40

Математика

Есть ответ 👍

Водном шкафу было в 3 раза меньше книг, чем в другом. когда в первый шкаф положили 17 книг, а из второго взяли 25, то в обоих шкафах книг стало поровну. сколько было книг в каждом шкафу?

107

192

Посмотреть ответы 3

Ответы на вопрос:

Leroy1234567

Математика

4,5(60 оценок)

ответ:

21 книга в первом шкафу

63 книг во втором шкафу

пошаговое объяснение:

х -книг в первом шкафу

3*х=3х книг во втором шкафу

составим уравнение

х+17=3х-25

17+25=3х-х

42=2х

х=42: 2

х=21 книга в первом шкафу

3*х=3*21=63 книг во втором шкафу

проверка:

21+17=63-25

38=38 верно

sharshukovauly

Математика

4,4(46 оценок)

ответ: 21 книга в первом шкафу

63 книг во втором шкафу

пошаговое объяснение:

х -книг в первом шкафу

3*х=3х книг во втором шкафу

составим уравнение

х+17=3х-25

17+25=3х-х

42=2х

х=42: 2

х=21 книга в первом шкафу

3*х=3*21=63 книг во втором шкафу

проверка:

21+17=63-25

38=38 верно

nastyak12119

Математика

4,7(75 оценок)

Пошаговое объяснение:

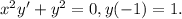
1) x^2y' +y^2 = 0, y(-1)=1.

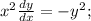
$x^2\frac{dy}{dx} = -y^2;$

Разделим переменные. При этом мы можем потерять решение 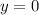y=0 , но т.к. оно не удовлетворяет дополнительному условию, то оно не будет являться искомым решением.

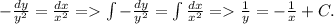$-\frac{dy}{y^2}=\frac{dx}{x^2} = \int -\frac{dy}{y^2}=\int \frac{dx}{x^2} = \frac{1}{y} = -\frac{1}{x}+C.$ Используем дополнительное условие для определения константы:

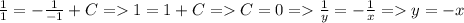
$\frac{1}{1}=-\frac{1}{-1} + C = 1 = 1 +C = C =0 = \frac{1}{y} = -\frac{1}{x} = y=-x$

ответ: 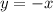y=-x

2) 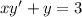xy'+y=3 . Так как это уравнение является линейным неоднородным, то решение можно искать в виде суммы общего решения линейного однородного уравнения и частного решения неоднородного уравнений: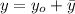 $y=y_o +\bar y$

Рассмотрим однородное уравнение:

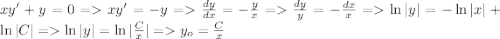
$xy'+y = 0 = xy'=-y = \frac{dy}{dx}=-\frac{y}{x} = \frac{dy}{y}=-\frac{dx}{x} = \ln|y|=-\ln|x|+\ln|C| = \ln|y|=\ln|\frac{C}{x}| = y_o=\frac{C}{x}$

(модули можно опустить без знака плюс-минус в следствие произвольности постоянной С. При делении на y мы могли потерять решение y=0, но оно входит в семейство кривых при С=0)

Частное решение неоднородного уравнения легко угадывается: 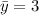$\bar y= 3$

Следовательно, общее решение исходного уравнения: 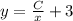$y = \frac{C}{x} + 3$

ответ: 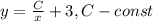$y=\frac{C}{x}+3, C - const$

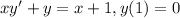
3) xy' + y = x+1, y(1) =0

Данное уравнение отличается от предыдущего только неоднородностью, поэтому нужно просто подобрать другое частное решение, удовлетворяющее неоднородности. Имеет смысл ее искать в виде: 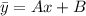$\bar y= Ax+B$ , подставим его в уравнение:

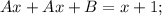
Ax + Ax + B = x +1;

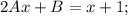
2Ax + B = x + 1;

Два полинома тождественно равны, если равны коэффициенты при соответствующих степенях:

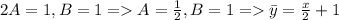
$2A = 1, B=1 = A=\frac{1}{2}, B=1 = \bar y = \frac{x}{2}+1$

Следовательно, общее решение исходного уравнения: 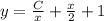$y= \frac{C}{x} +\frac{x}{2}+1$

Найдем константу из дополнительного условия:

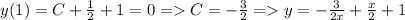
$y(1)=C + \frac{1}{2}+1 = 0 = C = -\frac{3}{2} = y=-\frac{3}{2x}+\frac{x}{2}+1$

ответ: 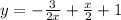$y=-\frac{3}{2x}+\frac{x}{2}+1$

4) xy'-y=3.

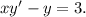
Применим алгоритм из пункта 2

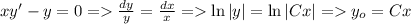
$xy'-y = 0 = \frac{dy}{y}=\frac{dx}{x} = \ln|y|=\ln|Cx| = y_o=Cx$

Частное решение неоднородного уравнения легко угадывается: 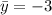$\bar y = -3$

Следовательно, общее решение исходного уравнения: 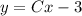y= Cx-3

ответ: 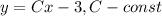y=Cx-3, C - const

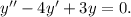
5) y''-4y'+3y=0.

Имеем дело с линейным однородным уравнением с постоянными коэффициентами. Его частные решения ищутся в виде: 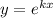$y = e^{kx}$ . Тогда характеристическое уравнение есть

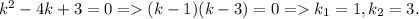
k^2-4k+3 =0 = (k-1)(k-3) =0 = k_1=1, k_2=3.

Общее решение такого уравнения записывается в виде линейной комбинации линейно независимых частных решений, экспоненты с неравными показателями являются линейно независимыми:

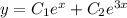
$y=C_1e^x+C_2e^{3x}$

ответ: 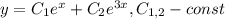$y=C_1e^x+C_2e^{3x}, C_{1,2} - const$

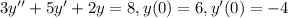
6) 3y''+5y'+2y=8, y(0)=6, y'(0)=-4

Общее решение является суммой общего решения однородного уравнения и частного решения неоднородного. Рассмотрим однородное: 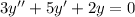3y''+5y'+2y=0

Характеристическое уравнение: 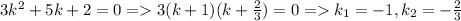$3k^2+5k+2=0 = 3(k+1)(k+\frac{2}{3})=0 = k_1=-1, k_2=-\frac{2}{3}$

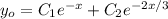
$y_o = C_1e^{-x} + C_2e^{-2x/3}$

Частное решение легко угадывается: 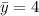$\bar y = 4$

Общее решение: 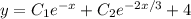$y= C_1e^{-x}+C_2e^{-2x/3}+4$

Определим постоянные из дополнительных условий:

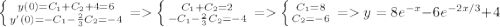
$\left \{ {{y(0)=C_1+C_2+4=6} \atop {y'(0)=-C_1-\frac{2}{3}C_2 = -4}} \right. = \left \{ {{C_1+C_2=2} \atop {-C_1-\frac{2}{3}C_2 = -4}} \right. = \left \{ {{C_1=8} \atop {C_2=-6}} \right. = y = 8e^{-x} -6e^{-2x/3}+4$

ответ: 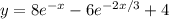$y=8e^{-x}-6e^{-2x/3}+4$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.