Математика: Найдите две последние цифры числа 2^2000

Дано: Найти: Решение. Вектор, представленный в пространстве в виде суммы единичных векторов (орт), то есть , где — числа, которые называются координатами вектора в некотором базисе, можно записать так: Таким образом, Умножение вектора на число имеет вид: Таким образом, и Для векторов и имеет место Таким образом, Длина вектора определяется как арифметический квадратный корень из суммы квадратов координат Таким образом, ответ:...

arinamal1

28.04.2021 19:38

Математика

Есть ответ 👍

Найдите две последние цифры числа 2^2000

108

254

Посмотреть ответы 2

Ответы на вопрос:

vladbortnovsij69

Математика

4,4(3 оценок)

будем возводить 2 в степень и смотреть последнюю цифру

2¹=2 ; 2²=4; 2³=8; 2⁴=16 дальше последние числа будут повторяться

2⁵=32; 2⁶=64; 2⁷=128; 2⁸=256

⇒ если возводить 2 в степень кратную 4 то последняя цифра будет 6

2²⁰⁰⁰=(2⁵⁰⁰)⁴ заканчивается на 6

Йошино1

Математика

4,4(51 оценок)

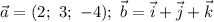
Дано: $\vec{a} = (2; ~ 3; ~ {-}4); ~ \vec{b} = \vec{i} + \vec{j} + \vec{k}$

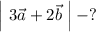
Найти: $\left|~3\vec{a} + 2\vec{b} ~ \right| - ?$

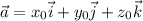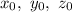Решение. Вектор, представленный в пространстве в виде суммы единичных векторов (орт), то есть $\vec{a} = x_{0}\vec{i} + y_{0}\vec{j} + z_{0}\vec{k}$ , где $x_{0}, ~ y_{0}, ~ z_{0}$ — числа, которые называются координатами вектора 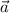$\vec{a}$ в некотором базисе, можно записать так: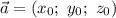 $\vec{a} = (x_{0}; ~ y_{0}; ~ z_{0})$

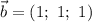
Таким образом, $\vec{b} = (1; ~ 1; ~ 1)$

Умножение вектора 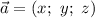$\vec{a} = (x; ~ y; ~ z)$ на число 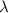$\lambda$ имеет вид: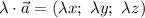 $\lambda \cdot \vec{a} = (\lambda x; ~ \lambda y; ~ \lambda z)$

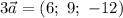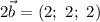
Таким образом, $3\vec{a} = (6; ~ 9; ~ {-}12)$ и $2\vec{b} = (2; ~ 2; ~ 2)$

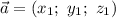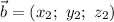Для векторов $\vec{a} = (x_{1}; ~ y_{1}; ~ z_{1})$ и $\vec{b} = (x_{2}; ~ y_{2}; ~ z_{2})$ имеет место $\vec{a} \pm \vec{b} = (x_{1} \pm x_{2}; ~ y_{1} \pm y_{2}; ~ z_{1} \pm z_{2})$

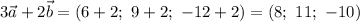
Таким образом, $3\vec{a} + 2\vec{b} = (6 + 2; ~ 9 + 2; ~ {-12} + 2) = (8; ~ 11; ~ {-}10)$

Длина вектора 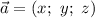$\vec{a} = (x; ~ y; ~ z)$ определяется как арифметический квадратный корень из суммы квадратов координат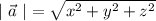 $\left|~\vec{a}~ \right| = \sqrt{x^{2} + y^{2} + z^{2}}$

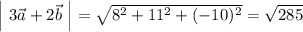
Таким образом, $\left|~3\vec{a} + 2\vec{b} ~ \right| = \sqrt{8^{2} + 11^{2} + (-10)^{2}} = \sqrt{285}$

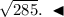
ответ: $\sqrt{285}. ~ \blacktriangleleft$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.